20. (本小题 8 分)
(1)因式分解:$-m^{3}n^{3}+8m^{2}n^{2}-16mn$; (2)解方程:$\frac{1}{x + 2}+\frac{4x}{x^{2} - 4}= \frac{2}{x - 2}$.
(1)因式分解:$-m^{3}n^{3}+8m^{2}n^{2}-16mn$; (2)解方程:$\frac{1}{x + 2}+\frac{4x}{x^{2} - 4}= \frac{2}{x - 2}$.
答案:
(1)
首先,从$-m^{3}n^{3}+8m^{2}n^{2}-16mn$中提取公因式$-mn$,得到:
$-mn(m^{2}n^{2}-8mn + 16)$
观察括号内的多项式$m^{2}n^{2}-8mn + 16$,它是一个完全平方公式,即$(mn - 4)^{2}$,
所以原式$=-mn(mn - 4)^{2}$。
(2)
给定方程$\frac{1}{x + 2}+\frac{4x}{x^{2} - 4}=\frac{2}{x - 2}$,
因为$x^{2}-4=(x + 2)(x - 2)$,
方程两边同乘$(x + 2)(x - 2)$去分母得:
$(x - 2)+4x=2(x + 2)$
去括号得:$x - 2+4x=2x + 4$
移项得:$x+4x-2x=4 + 2$
合并同类项得:$3x=6$
系数化为$1$得:$x=2$
检验:当$x = 2$时,$(x + 2)(x - 2)=(2 + 2)×(2 - 2)=0$,
所以$x = 2$是增根,原方程无解。
(1)
首先,从$-m^{3}n^{3}+8m^{2}n^{2}-16mn$中提取公因式$-mn$,得到:
$-mn(m^{2}n^{2}-8mn + 16)$
观察括号内的多项式$m^{2}n^{2}-8mn + 16$,它是一个完全平方公式,即$(mn - 4)^{2}$,
所以原式$=-mn(mn - 4)^{2}$。
(2)
给定方程$\frac{1}{x + 2}+\frac{4x}{x^{2} - 4}=\frac{2}{x - 2}$,
因为$x^{2}-4=(x + 2)(x - 2)$,
方程两边同乘$(x + 2)(x - 2)$去分母得:
$(x - 2)+4x=2(x + 2)$
去括号得:$x - 2+4x=2x + 4$
移项得:$x+4x-2x=4 + 2$
合并同类项得:$3x=6$
系数化为$1$得:$x=2$
检验:当$x = 2$时,$(x + 2)(x - 2)=(2 + 2)×(2 - 2)=0$,
所以$x = 2$是增根,原方程无解。
21. (本小题 10 分)
如图,在$\triangle ABC$中,$BE是\triangle ABC$的角平分线,$DE// BC$,交$AB于点D$.若$\angle A = 65^{\circ}$,$\angle BEC = 95^{\circ}$,求$\angle DEB$的度数.
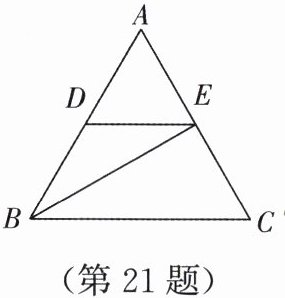
如图,在$\triangle ABC$中,$BE是\triangle ABC$的角平分线,$DE// BC$,交$AB于点D$.若$\angle A = 65^{\circ}$,$\angle BEC = 95^{\circ}$,求$\angle DEB$的度数.

答案:
在△ABC中,∠A=65°,则∠ABC+∠ACB=180°-65°=115°。
设∠ABE=∠CBE=x(BE是角平分线),则∠ABC=2x,∠ACB=115°-2x。
在△BEC中,∠BEC=95°,∠EBC=x,∠ECB=∠ACB=115°-2x,由内角和定理得:
x + 95° + (115° - 2x) = 180°
解得x=30°,即∠EBC=30°。
∵DE//BC,
∴∠DEB=∠EBC=30°(内错角相等)。
∠DEB=30°
设∠ABE=∠CBE=x(BE是角平分线),则∠ABC=2x,∠ACB=115°-2x。
在△BEC中,∠BEC=95°,∠EBC=x,∠ECB=∠ACB=115°-2x,由内角和定理得:
x + 95° + (115° - 2x) = 180°
解得x=30°,即∠EBC=30°。
∵DE//BC,
∴∠DEB=∠EBC=30°(内错角相等)。
∠DEB=30°
查看更多完整答案,请扫码查看


