19. (本小题 10 分)
如图,△ABC 的角平分线 BP 与外角∠ACD 的平分线 CP 相交于点 P. 解答下列问题:
(1)若∠ABC = 50°,∠ACB = 80°,求∠P 的度数;
(2)结合题(1)的计算,确定∠P 与∠BAC 的数量关系,并说明理由.

如图,△ABC 的角平分线 BP 与外角∠ACD 的平分线 CP 相交于点 P. 解答下列问题:
(1)若∠ABC = 50°,∠ACB = 80°,求∠P 的度数;
(2)结合题(1)的计算,确定∠P 与∠BAC 的数量关系,并说明理由.

答案:
(1)在△ABC中,∠ACB=80°,∠ACD为外角,
∴∠ACD=180°-∠ACB=100°.
∵CP平分∠ACD,
∴∠PCD=∠ACD/2=50°.
∵BP平分∠ABC,∠ABC=50°,
∴∠PBC=∠ABC/2=25°.
∵∠PCD是△PBC的外角,
∴∠PCD=∠PBC+∠P.
∴∠P=∠PCD-∠PBC=50°-25°=25°.
(2)∠P=1/2∠BAC.
理由:设∠BAC=α.
∵∠ACD是△ABC的外角,
∴∠ACD=∠BAC+∠ABC=α+∠ABC.
∵CP平分∠ACD,
∴∠PCD=∠ACD/2=(α+∠ABC)/2.
∵BP平分∠ABC,
∴∠PBC=∠ABC/2.
∵∠PCD是△PBC的外角,
∴∠PCD=∠PBC+∠P.
∴∠P=∠PCD-∠PBC=(α+∠ABC)/2 - ∠ABC/2=α/2.
即∠P=1/2∠BAC.
(1)在△ABC中,∠ACB=80°,∠ACD为外角,
∴∠ACD=180°-∠ACB=100°.
∵CP平分∠ACD,
∴∠PCD=∠ACD/2=50°.
∵BP平分∠ABC,∠ABC=50°,
∴∠PBC=∠ABC/2=25°.
∵∠PCD是△PBC的外角,
∴∠PCD=∠PBC+∠P.
∴∠P=∠PCD-∠PBC=50°-25°=25°.
(2)∠P=1/2∠BAC.
理由:设∠BAC=α.
∵∠ACD是△ABC的外角,
∴∠ACD=∠BAC+∠ABC=α+∠ABC.
∵CP平分∠ACD,
∴∠PCD=∠ACD/2=(α+∠ABC)/2.
∵BP平分∠ABC,
∴∠PBC=∠ABC/2.
∵∠PCD是△PBC的外角,
∴∠PCD=∠PBC+∠P.
∴∠P=∠PCD-∠PBC=(α+∠ABC)/2 - ∠ABC/2=α/2.
即∠P=1/2∠BAC.
20. (本小题 10 分)
如图,在△ABC 中,BE 平分∠ABC,点 P 在射线 BE 上.
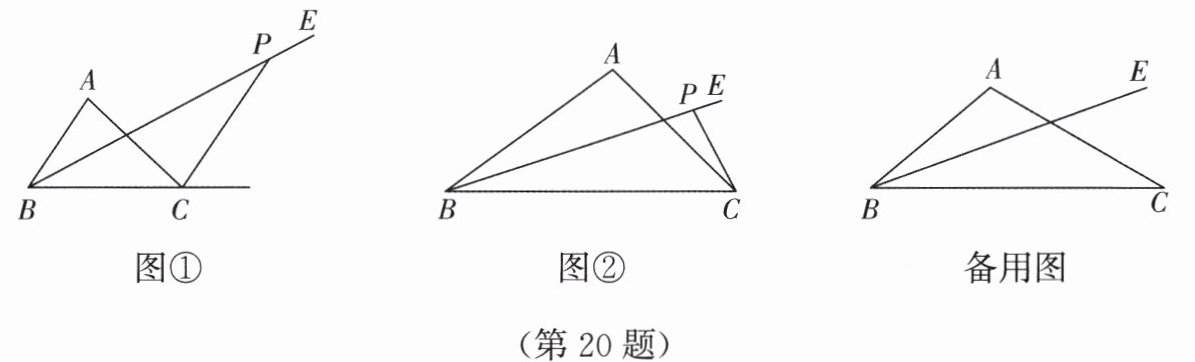
(1)如图①,连接 CP,若∠ABC = 56°,CP // AB,求∠BPC 的度数;
(2)如图②,连接 CP,若∠A = 100°,∠PBC = ∠PCA,求∠BPC 的度数;
(3)若∠ABC = 40°,∠ACB = 30°,直线 CP 与△ABC 的一条边垂直,求∠BPC 的度数.(直接写出结果)
如图,在△ABC 中,BE 平分∠ABC,点 P 在射线 BE 上.

(1)如图①,连接 CP,若∠ABC = 56°,CP // AB,求∠BPC 的度数;
(2)如图②,连接 CP,若∠A = 100°,∠PBC = ∠PCA,求∠BPC 的度数;
(3)若∠ABC = 40°,∠ACB = 30°,直线 CP 与△ABC 的一条边垂直,求∠BPC 的度数.(直接写出结果)
答案:
(1)
∵BE平分∠ABC,∠ABC=56°,
∴∠PBC=∠ABC/2=28°。
∵CP//AB,
∴∠BPC=∠PBC=28°(内错角相等)。
故∠BPC=28°。
(2)设∠PBC=∠PCA=x,
∵BE平分∠ABC,
∴∠ABC=2x。
在△ABC中,∠A=100°,
∴∠ABC+∠ACB=80°,即2x+∠ACB=80°,
∴∠ACB=80°-2x。
∵∠ACB=∠PCA+∠PCB,
∴∠PCB=∠ACB-x=80°-3x。
在△BPC中,∠BPC=180°-∠PBC-∠PCB=180°-x-(80°-3x)=100°。
故∠BPC=100°。
(3)40°或70°或100°或110°。
(1)
∵BE平分∠ABC,∠ABC=56°,
∴∠PBC=∠ABC/2=28°。
∵CP//AB,
∴∠BPC=∠PBC=28°(内错角相等)。
故∠BPC=28°。
(2)设∠PBC=∠PCA=x,
∵BE平分∠ABC,
∴∠ABC=2x。
在△ABC中,∠A=100°,
∴∠ABC+∠ACB=80°,即2x+∠ACB=80°,
∴∠ACB=80°-2x。
∵∠ACB=∠PCA+∠PCB,
∴∠PCB=∠ACB-x=80°-3x。
在△BPC中,∠BPC=180°-∠PBC-∠PCB=180°-x-(80°-3x)=100°。
故∠BPC=100°。
(3)40°或70°或100°或110°。
查看更多完整答案,请扫码查看


