《2025年学习质量监测八年级数学上册人教版》

25. (本小题 10 分)
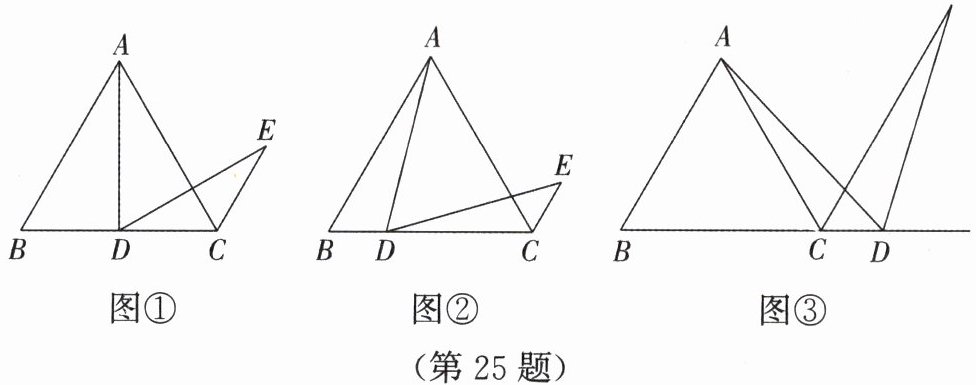
已知$\triangle ABC$是等边三角形,点$D在直线BC$上,$\angle ADE = 60^{\circ}$,$AD = DE$,连接$CE$.
(1)当点$D在线段BC$上时,
①如图 1,当$D是线段BC$的中点时,判断线段$BD与CE$的数量关系,请直接写出结论(不必证明)；
②如图 2,当$D是线段BC$上的任意一点时,请用等式表示线段$AB$,$CE$,$CD$之间的数量关系,并证明.
(2)如图 3,当点$D在线段BC$的延长线上时,$\angle ADE = 60^{\circ}$,$AD = DE$.若$BC = 4$,$CD = 1$,求线段$CE$的长.

答案：
(1)① BD=CE
(2)② AB=CE+CD
证明：
∵△ABC是等边三角形，
∴AB=AC，∠BAC=60°。
∵AD=DE，∠ADE=60°，
∴△ADE是等边三角形，
∴AD=AE，∠DAE=60°。
∴∠BAC=∠DAE，
∴∠BAC-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE。
在△ABD和△ACE中，
$\left\{\begin{array}{l} AB=AC \\ ∠BAD=∠CAE \\ AD=AE \end{array}\right.$
∴△ABD≌△ACE(SAS)，
∴BD=CE。
∵点D在线段BC上，
∴BC=BD+CD。
∵AB=BC，
∴AB=CE+CD。
(2)
∵△ABC是等边三角形，
∴AB=AC=BC=4，∠BAC=60°。
∵AD=DE，∠ADE=60°，
∴△ADE是等边三角形，
∴AD=AE，∠DAE=60°。
∴∠BAC=∠DAE，
∴∠BAC+∠CAD=∠DAE+∠CAD，即∠BAD=∠CAE。
在△ABD和△ACE中，
$\left\{\begin{array}{l} AB=AC \\ ∠BAD=∠CAE \\ AD=AE \end{array}\right.$
∴△ABD≌△ACE(SAS)，
∴BD=CE。
∵点D在线段BC的延长线上，BC=4，CD=1，
∴BD=BC+CD=4+1=5，
∴CE=5。