7. 如图,在 $Rt \triangle ABC$ 中,$\angle C = 90^{\circ}$,$AD$ 是角平分线,$DE \perp AB$ 于点 $E$,下列结论错误的是(
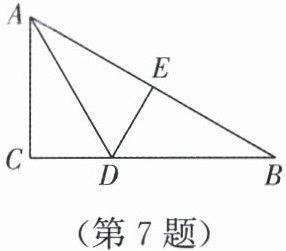
A.$BD + DE = BC$
B.$DE$ 平分 $\angle ADB$
C.$DA$ 平分 $\angle EDC$
D.$DE + AC > AD$
B
).
A.$BD + DE = BC$
B.$DE$ 平分 $\angle ADB$
C.$DA$ 平分 $\angle EDC$
D.$DE + AC > AD$
答案:
B
8. 如图,已知在 $\triangle PAB$ 中,$\angle A = \angle B$,$M$,$N$,$K$ 分别是 $PA$,$PB$,$AB$ 上的点,且 $AM = BK$,$BN = AK$. 若 $\angle MKN = 42^{\circ}$,则 $\angle P$ 的度数为(
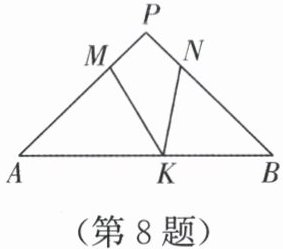
A.$44^{\circ}$
B.$66^{\circ}$
C.$96^{\circ}$
D.$92^{\circ}$
C
).
A.$44^{\circ}$
B.$66^{\circ}$
C.$96^{\circ}$
D.$92^{\circ}$
答案:
C
9. 如图,点 $A$ 在 $DE$ 上,$AB$ 交 $CD$ 于点 $F$,且 $AC = CE$,$\angle 1 = \angle 2 = \angle 3$,则 $DE$ 的长等于(
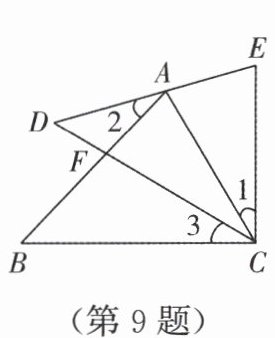
A.$AC$
B.$BC$
C.$AB + AC$
D.$AB$
D
).
A.$AC$
B.$BC$
C.$AB + AC$
D.$AB$
答案:
D
10. 课外兴趣小组活动时,老师提出了如下问题:如图,在 $\triangle ABC$ 中,$AB = 8$,$AC = 6$,求 $BC$ 边上的中线 $AD$ 的取值范围. 小明在组内经过合作交流,得到了如下的解决方法:延长 $AD$ 至点 $E$,使 $DE = AD$,连接 $BE$. 请根据小明的方法进行思考,求得 $AD$ 的取值范围是(
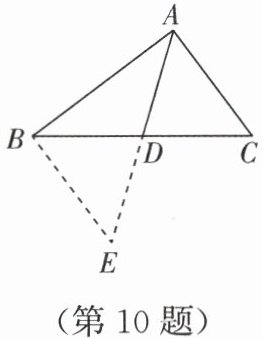
A.$6 < AD < 8$
B.$6 \leq AD \leq 8$
C.$1 < AD < 7$
D.$1 \leq AD \leq 7$
C
).
A.$6 < AD < 8$
B.$6 \leq AD \leq 8$
C.$1 < AD < 7$
D.$1 \leq AD \leq 7$
答案:
C
11. 两组邻边分别相等的四边形叫作“筝形”. 如图,四边形 $ABCD$ 是一个筝形,其中 $AD = CD$,$AB = CB$. 晓明同学在探究筝形的性质时,得到如下结论:①$\triangle ABD \cong \triangle CBD$;②$AO = CO = \frac{1}{2}AC$;③$AC \perp BD$. 其中,正确的结论有
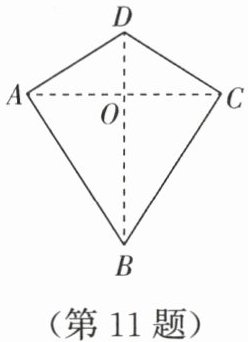
3
个.
答案:
3
12. 如图,已知 $\triangle ABC \cong \triangle ADE$,$\angle B = 63^{\circ}$,$\angle C = 27^{\circ}$,则 $\angle DAE$ 的大小为
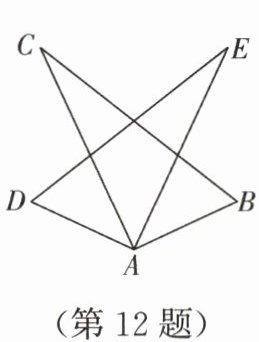
90°
.
答案:
90°
查看更多完整答案,请扫码查看


