《2025年点拨训练七年级数学上册沪科版安徽专版》

21. 将连续的奇数1,3,5,7,9,…排列成如图所示的数阵：

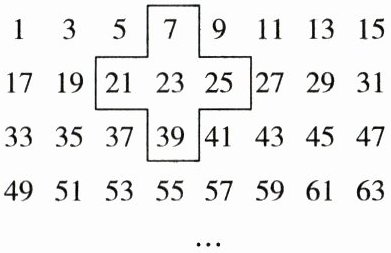
(1)十字框中的五个数的和是115,是中间数23的5倍.
(2)十字框中的五个数之和能等于2025吗？若能,请写出这五个数；若不能,请说明理由.
能.这五个数分别是389,403,405,407,421.

答案：
(1)115；5
(2)能.这五个数分别是389,403,405,407,421.

22. 我们规定,关于$x$,$y的二元一次方程ax + by = c$,若满足$a + b = c$,则称这个方程为“最佳”方程. 例如：方程$3x + 4y = 7$,其中$a = 3$,$b = 4$,$c = 7$,满足$a + b = c$,则方程$3x + 4y = 7$是“最佳”方程,把两个“最佳”方程合在一起叫“最佳”方程组. 根据上述规定,回答下列问题：
(1)方程$3x + 6y = 9$是(填“是”或“不是”)“最佳”方程；
(2)若关于$x$,$y的二元一次方程kx + (2k - 1)y = 11$是“最佳”方程,求$k$的值；
$k=4$.
(3)若$\begin{cases}x = p, \\ y = q\end{cases} 是关于x$,$y$的“最佳”方程组$\begin{cases}nx + (m - 3)y = 2 - m, \\ mx + (n + 1)y = 2m + 3\end{cases} $的解,求$2p + 3q$的值.
$2p+3q=5.$

答案：
(1)是
(2)$k=4$.
(3)$2p+3q=5.$