16. 计算:
(1)$(-1)^{3} - \frac{5}{4}×\frac{4}{9}÷[1 + 2×(-3)]$;
(2)$(-\frac{3}{4} + \frac{7}{12} - \frac{5}{6})×(-36)$.
(1)$(-1)^{3} - \frac{5}{4}×\frac{4}{9}÷[1 + 2×(-3)]$;
(2)$(-\frac{3}{4} + \frac{7}{12} - \frac{5}{6})×(-36)$.
答案:
(1)原式$=-\dfrac{8}{9}$.
(2)原式$=36$.
(1)原式$=-\dfrac{8}{9}$.
(2)原式$=36$.
17. 将下列各数表示在如图所示的数轴上,并用“<”号连接起来:
$-|-3|$,$-(-4)$,0,$-1\frac{1}{3}$,1.5
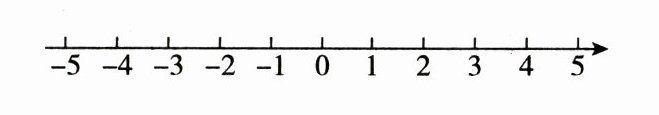
$-|-3|$,$-(-4)$,0,$-1\frac{1}{3}$,1.5
答案:
解:$-|-3|=-3,-(-4)=4$.
$-|-3|<-1\dfrac{1}{3}<0<1.5<-(-4)$.
$-|-3|<-1\dfrac{1}{3}<0<1.5<-(-4)$.
18. 先化简,再求值:$-2a^{2}b + 2(3ab^{2} - a^{2}b) - 3(2ab^{2} - a^{2}b)$,其中$a = 2$,$b = -3$.
答案:
解:原式$=-a^{2}b$,当$a=2,b=-3$时,原式$=12$.
查看更多完整答案,请扫码查看


