《2025年数学实验手册九年级全一册》

1. 探索角度的变化
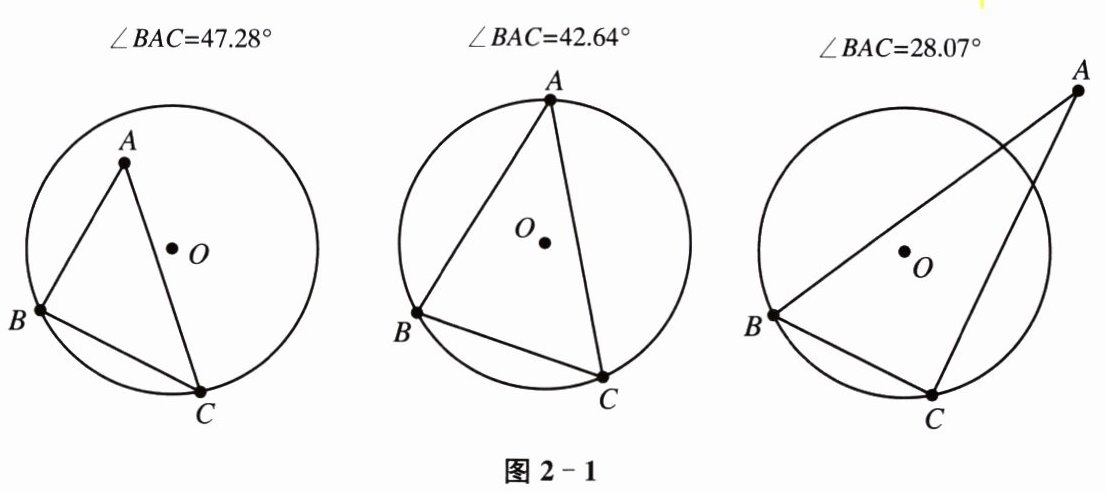
打开动态几何软件,画$\odot O$,在$\odot O$上任取两点 B、C.在平面内任取一点 A,连接 AB、AC、BC,度量$\angle BAC$的度数.
如图 2-1,在 BC 的一侧拖动点 A,观察当点 A 分别在圆内、圆上、圆外时,$\angle BAC$的度数变化情况.你有什么发现？

答案： 【解析】：本题主要考查圆周角定理，即同弧所对的圆周角等于圆心角的一半，以及圆内接四边形的性质。
通过观察动态几何软件中，当点A在圆内、圆上、圆外时，$\angle BAC$的度数变化情况，来探索圆周角与圆心角之间的关系。
当点A在圆上时，$\angle BAC$是圆周角，它所对应的是弧BC。
根据圆周角定理，同弧所对的圆周角是圆心角的一半。
因此，当点A在圆上时，$\angle BAC$的度数是固定的，且等于弧BC所对的圆周角。
当点A在圆内时，可以通过连接圆心O与点A，并延长交圆于点D，来构造两个圆周角$\angle DBC$和$\angle DCB$，它们分别对应弧DC和弧DB。
由于$\angle BAC$是这两个圆周角的外角，根据外角定理，$\angle BAC$等于两个不相邻的内角之和，即$\angle BAC = \angle DBC + \angle DCB$。
因此，当点A在圆内时，$\angle BAC$的度数会大于它所对应的任何一个个圆周角的度数，所以此时$\angle BAC$的度数会大于点A在圆上时的度数。
当点A在圆外时，可以通过连接圆心O与点A，交圆于点E，来构造一个圆内接四边形ABEC。
根据圆内接四边形的性质，对角互补，即$\angle BAC + \angle BEC = 180^\circ$。
由于$\angle BEC$是圆周角，它等于弧BC所对的圆周角的一半，因此当点A在圆外时，$\angle BAC$的度数会小于$180^\circ$减去弧BC所对的圆周角的度数，所以此时$\angle BAC$的度数会小于点A在圆上时的度数。
综上所述，可以发现：当点A在圆上时，$\angle BAC$的度数等于弧BC所对的圆周角的度数；当点A在圆内时，$\angle BAC$的度数大于弧BC所对的圆周角的度数；当点A在圆外时，$\angle BAC$的度数小于弧BC所对的圆周角的度数。
【答案】：发现：当点A在圆上时，$\angle BAC$的度数等于弧BC所对的圆周角的度数；当点A在圆内时，$\angle BAC$的度数大于弧BC所对的圆周角的度数；当点A在圆外时，$\angle BAC$的度数小于弧BC所对的圆周角的度数。