《2025年数学实验手册九年级全一册》

3. 探索二次函数 $ y= ax^{2} $ 的图像和 $ y= a(x-h)^{2}+k $ 的图像之间的关系
(1) 用透明纸片探究.
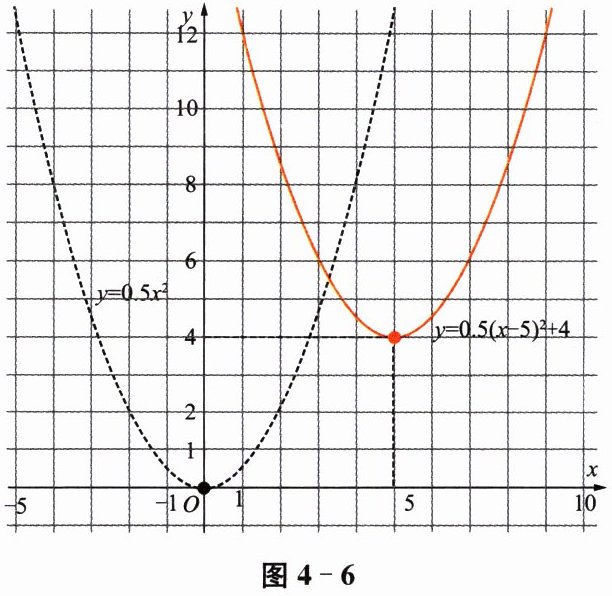
将透明纸片上二次函数 $ y= 0.5x^{2} $ 的图像与图 4-6 中的二次函数 $ y= 0.5x^{2} $ 的图像(虚线图)重合,把透明纸片沿 x 轴向右平移 5 个单位长度,再沿过点(5,0)且平行于 y 轴的直线向上平移 4 个单位长度.你有什么发现？

(2) 用动态几何软件探究.
打开动态几何软件,建立平面直角坐标系.按照上述画二次函数图像的方法,画二次函数 $ y= ax^{2} $、$ y= a(x-h)^{2}+k $ 的图像.探究二次函数 $ y= a(x-h)^{2}+k $ 的图像与二次函数 $ y= ax^{2} $ 的图像之间的关系.
思考:二次函数 $ y= ax^{2}+bx+c $ 的图像如何由二次函数 $ y= ax^{2} $ 的图像平移得到？

答案：
(1) 透明纸片上的图像与图中$y=0.5(x-5)^{2}+4$的图像重合。
(2) 二次函数$y=a(x-h)^{2}+k$的图像是由$y=ax^{2}$的图像沿$x$轴向右（$h＞0$）或向左（$h＜0$）平移$|h|$个单位长度，再沿$y$轴向上（$k＞0$）或向下（$k＜0$）平移$|k|$个单位长度得到的。
思考：将$y=ax^{2}+bx+c$配方得$y=a\left(x+\dfrac{b}{2a}\right)^{2}+\dfrac{4ac-b^{2}}{4a}$，故其图像是由$y=ax^{2}$的图像沿$x$轴向左（$b＞0$）或向右（$b＜0$）平移$\left|\dfrac{b}{2a}\right|$个单位长度，再沿$y$轴向上（$\dfrac{4ac-b^{2}}{4a}＞0$）或向下（$\dfrac{4ac-b^{2}}{4a}＜0$）平移$\left|\dfrac{4ac-b^{2}}{4a}\right|$个单位长度得到的。