2025年数学实验手册九年级全一册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年数学实验手册九年级全一册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
2. 计算与估计
测量图 13-1 中圆的半径,并计算各正多边形的周长与圆的直径的比值.随着正多边形边数的增加,它们的周长与圆的直径的比值有怎样的变化趋势?
测量图 13-1 中圆的半径,并计算各正多边形的周长与圆的直径的比值.随着正多边形边数的增加,它们的周长与圆的直径的比值有怎样的变化趋势?
答案:
【解析】:
本题考查的是对圆周率的理解以及正多边形与圆的关系。
首先,需要明确,当我们将一个圆等分成若干份,并用这些等份作顶点可以作出一个正多边形,这个正多边形的周长会随着等份的增多(即边数的增多)而逐渐接近圆的周长。
在本题中,我们需要通过实际测量或理论推导来得出圆的半径,并据此计算出正多边形的周长以及圆的直径。然后,我们比较正多边形的周长与圆的直径的比值。
理论上,随着正多边形边数的增加,正多边形的周长会越来越接近圆的周长,因此,正多边形的周长与圆的直径的比值也会越来越接近圆周率π(即圆的周长与直径的比值)。
由于本题是实验题,且未给出具体的圆半径测量值和多边形边数,因此无法给出具体的数值答案,但可以确定的是,正多边形的周长与圆的直径的比值将随着边数的增加而趋近于π。
【答案】:
由于本题是实验探究题,且未给出具体测量数据和多边形边数,因此无法给出具体数值答案。但可以确定的变化趋势是:随着正多边形边数的增加,它们的周长与圆的直径的比值将越来越接近圆周率π。
本题考查的是对圆周率的理解以及正多边形与圆的关系。
首先,需要明确,当我们将一个圆等分成若干份,并用这些等份作顶点可以作出一个正多边形,这个正多边形的周长会随着等份的增多(即边数的增多)而逐渐接近圆的周长。
在本题中,我们需要通过实际测量或理论推导来得出圆的半径,并据此计算出正多边形的周长以及圆的直径。然后,我们比较正多边形的周长与圆的直径的比值。
理论上,随着正多边形边数的增加,正多边形的周长会越来越接近圆的周长,因此,正多边形的周长与圆的直径的比值也会越来越接近圆周率π(即圆的周长与直径的比值)。
由于本题是实验题,且未给出具体的圆半径测量值和多边形边数,因此无法给出具体的数值答案,但可以确定的是,正多边形的周长与圆的直径的比值将随着边数的增加而趋近于π。
【答案】:
由于本题是实验探究题,且未给出具体测量数据和多边形边数,因此无法给出具体数值答案。但可以确定的变化趋势是:随着正多边形边数的增加,它们的周长与圆的直径的比值将越来越接近圆周率π。
3. 探究圆周率的近似值
(1) 画圆的内接正十二边形.
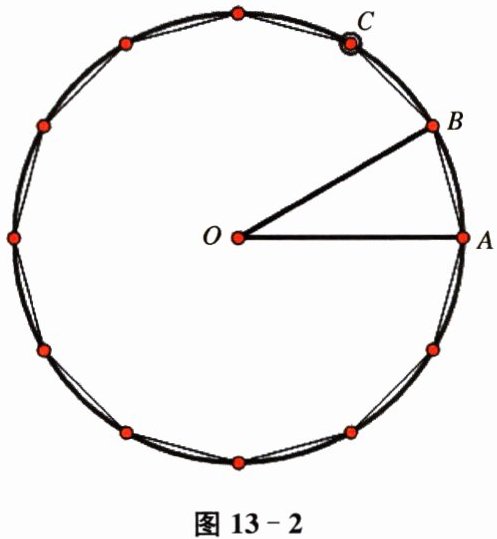
打开动态几何软件,画$\odot O$,并将$\odot O$十二等分,得到圆的十二等分点 A、B、C……;顺次连接 AB、BC……得到$\odot O$的内接正十二边形(如图 13-2).
度量线段 AB、OA,并计算$\frac{12AB}{2OA}$的值.
(2) 画圆的内接正二十四边形.
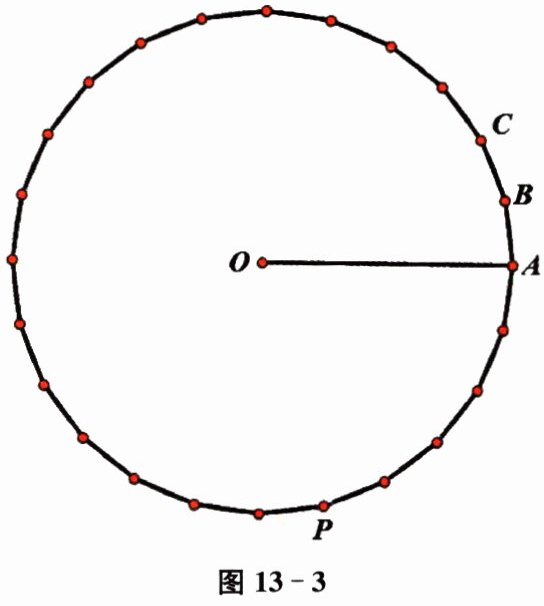
打开动态几何软件,仿照 3(1)中的画图方法,画出圆的内接正二十四边形(如图 13-3),计算圆的内接正二十四边形的周长与圆的直径的比值.
(3) 通过上面的操作与计算,你有什么发现?
(4) 如果继续增加圆的等分点个数呢?
(1) 画圆的内接正十二边形.
打开动态几何软件,画$\odot O$,并将$\odot O$十二等分,得到圆的十二等分点 A、B、C……;顺次连接 AB、BC……得到$\odot O$的内接正十二边形(如图 13-2).
度量线段 AB、OA,并计算$\frac{12AB}{2OA}$的值.

(2) 画圆的内接正二十四边形.
打开动态几何软件,仿照 3(1)中的画图方法,画出圆的内接正二十四边形(如图 13-3),计算圆的内接正二十四边形的周长与圆的直径的比值.

(3) 通过上面的操作与计算,你有什么发现?
(4) 如果继续增加圆的等分点个数呢?
答案:
(1) 解:通过动态几何软件度量计算,$\frac{12AB}{2OA}\approx3.1058$。
(2) 解:通过动态几何软件度量计算,圆的内接正二十四边形的周长与圆的直径的比值约为$3.1326$。
(3) 解:圆的内接正多边形的边数越多,其周长与圆的直径的比值越接近圆周率$\pi$。
(4) 解:继续增加圆的等分点个数,即增加内接正多边形的边数,该比值会更接近圆周率$\pi$。
(1) 解:通过动态几何软件度量计算,$\frac{12AB}{2OA}\approx3.1058$。
(2) 解:通过动态几何软件度量计算,圆的内接正二十四边形的周长与圆的直径的比值约为$3.1326$。
(3) 解:圆的内接正多边形的边数越多,其周长与圆的直径的比值越接近圆周率$\pi$。
(4) 解:继续增加圆的等分点个数,即增加内接正多边形的边数,该比值会更接近圆周率$\pi$。
查看更多完整答案,请扫码查看


