2025年数学实验手册九年级全一册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年数学实验手册九年级全一册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 探索二次函数 $ y= ax^{2} $ 的图像和 $ y= ax^{2}+k $ 的图像之间的关系
(1) 用透明纸片探究.
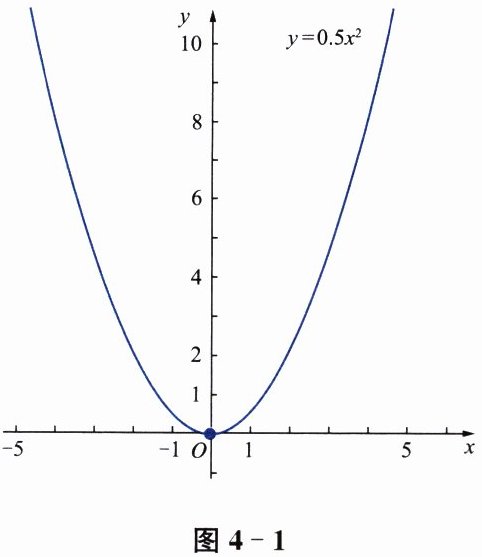
剪下附录 B 中如图 4-1 所示的透明纸片.将透明纸片上的二次函数 $ y= 0.5x^{2} $ 的图像与图 4-2 中的二次函数 $ y= 0.5x^{2} $ 的图像(虚线图)重合,把透明纸片沿 y 轴向上平移 4 个单位长度.你有什么发现?请通过计算验证你的发现.
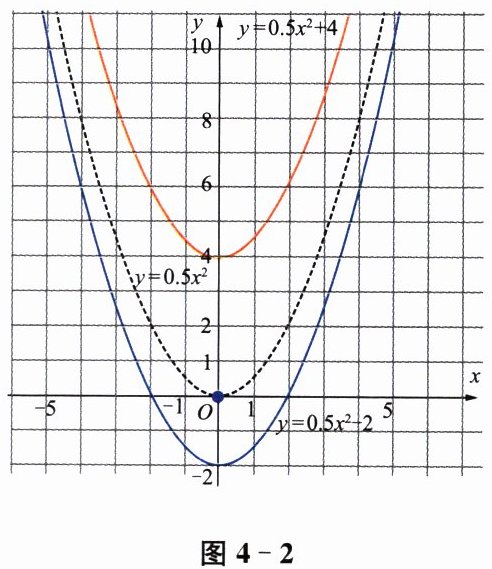
将透明纸片上二次函数 $ y= 0.5x^{2} $ 的图像与图 4-2 中的二次函数 $ y= 0.5x^{2} $ 的图像(虚线图)重合,把透明纸片沿 y 轴向下平移 2 个单位长度.你有什么发现?请通过计算验证你的发现.
(2) 用动态几何软件探究.
打开动态几何软件,在 x 轴上任取一点 A,用字母 a 表示点 A 的横坐标,在 y 轴上任取一点 K,用字母 k 表示点 K 的纵坐标,画二次函数 $ y= ax^{2} $ 的图像和 $ y= ax^{2}+k $ 的图像,如图 4-3 所示.

在 x 轴上任取一点 M,过点 M 画 x 轴的垂线 l,直线 l 分别交二次函数 $ y= ax^{2} $ 与 $ y= ax^{2}+k $ 的图像于点 C、D.度量并计算点 C、D 的纵坐标之差,你有什么发现?
移动点 A、K,改变 a、k 的值,再移动点 M,观察点 C、D 的纵坐标之差有何变化.
思考:二次函数 $ y= ax^{2}+k $ 的图像如何由二次函数 $ y= ax^{2} $ 的图像平移得到?
(1) 用透明纸片探究.
剪下附录 B 中如图 4-1 所示的透明纸片.将透明纸片上的二次函数 $ y= 0.5x^{2} $ 的图像与图 4-2 中的二次函数 $ y= 0.5x^{2} $ 的图像(虚线图)重合,把透明纸片沿 y 轴向上平移 4 个单位长度.你有什么发现?请通过计算验证你的发现.


将透明纸片上二次函数 $ y= 0.5x^{2} $ 的图像与图 4-2 中的二次函数 $ y= 0.5x^{2} $ 的图像(虚线图)重合,把透明纸片沿 y 轴向下平移 2 个单位长度.你有什么发现?请通过计算验证你的发现.
(2) 用动态几何软件探究.
打开动态几何软件,在 x 轴上任取一点 A,用字母 a 表示点 A 的横坐标,在 y 轴上任取一点 K,用字母 k 表示点 K 的纵坐标,画二次函数 $ y= ax^{2} $ 的图像和 $ y= ax^{2}+k $ 的图像,如图 4-3 所示.

在 x 轴上任取一点 M,过点 M 画 x 轴的垂线 l,直线 l 分别交二次函数 $ y= ax^{2} $ 与 $ y= ax^{2}+k $ 的图像于点 C、D.度量并计算点 C、D 的纵坐标之差,你有什么发现?
移动点 A、K,改变 a、k 的值,再移动点 M,观察点 C、D 的纵坐标之差有何变化.
思考:二次函数 $ y= ax^{2}+k $ 的图像如何由二次函数 $ y= ax^{2} $ 的图像平移得到?
答案:
【解析】:
本题主要考察二次函数图像的平移性质。
对于函数$y = ax^{2} + k$,当$a$保持不变,$k$发生变化时,函数的图像会沿着$y$轴进行上下平移。
具体地,当$k$增大时,图像向上平移;当$k$减小时,图像向下平移。
(1)用透明纸片探究:
剪下附录B中如图4-1所示的透明纸片,将透明纸片上的二次函数$y = 0.5x^{2}$的图像与图4-2中的二次函数$y = 0.5x^{2}$的图像(虚线图)重合。
把透明纸片沿$y$轴向上平移4个单位长度,发现图像上的每一点都向上移动了4个单位长度,即函数值增加了4,这验证了函数$y = 0.5x^{2} + 4$的图像是由$y = 0.5x^{2}$的图像向上平移4个单位长度得到的。
同样地,把透明纸片沿$y$轴向下平移2个单位长度,发现图像上的每一点都向下移动了2个单位长度,即函数值减少了2,这验证了函数$y = 0.5x^{2} - 2$的图像是由$y = 0.5x^{2}$的图像向下平移2个单位长度得到的。
(2)用动态几何软件探究:
打开动态几何软件,在$x$轴上任取一点A,用字母$a$表示点A的横坐标,在$y$轴上任取一点K,用字母$k$表示点K的纵坐标。
画二次函数$y = ax^{2}$的图像和$y = ax^{2} + k$的图像。
在$x$轴上任取一点M,过点M画$x$轴的垂线l,直线l分别交二次函数$y = ax^{2}$与$y = ax^{2} + k$的图像于点C、D。
度量并计算点C、D的纵坐标之差,发现这个差值就是$k$,即函数$y = ax^{2} + k$与$y = ax^{2}$的图像在相同$x$值下的$y$值之差。
移动点A、K,改变$a$、$k$的值,再移动点M,观察点C、D的纵坐标之差,发现无论$a$、$k$和$x$如何变化,这个差值始终等于$k$。
思考:二次函数$y = ax^{2} + k$的图像如何由二次函数$y = ax^{2}$的图像平移得到?
答:当$k > 0$时,二次函数$y = ax^{2} + k$的图像由二次函数$y = ax^{2}$的图像向上平移$k$个单位长度得到;当$k < 0$时,二次函数$y = ax^{2} + k$的图像由二次函数$y = ax^{2}$的图像向下平移$|k|$个单位长度得到。
【答案】:
(1) 发现图像沿$y$轴上下平移,计算验证了平移规律;
(2) 发现点C、D的纵坐标之差为$k$,思考得出二次函数$y = ax^{2} + k$的图像由二次函数$y = ax^{2}$的图像平移得到。
本题主要考察二次函数图像的平移性质。
对于函数$y = ax^{2} + k$,当$a$保持不变,$k$发生变化时,函数的图像会沿着$y$轴进行上下平移。
具体地,当$k$增大时,图像向上平移;当$k$减小时,图像向下平移。
(1)用透明纸片探究:
剪下附录B中如图4-1所示的透明纸片,将透明纸片上的二次函数$y = 0.5x^{2}$的图像与图4-2中的二次函数$y = 0.5x^{2}$的图像(虚线图)重合。
把透明纸片沿$y$轴向上平移4个单位长度,发现图像上的每一点都向上移动了4个单位长度,即函数值增加了4,这验证了函数$y = 0.5x^{2} + 4$的图像是由$y = 0.5x^{2}$的图像向上平移4个单位长度得到的。
同样地,把透明纸片沿$y$轴向下平移2个单位长度,发现图像上的每一点都向下移动了2个单位长度,即函数值减少了2,这验证了函数$y = 0.5x^{2} - 2$的图像是由$y = 0.5x^{2}$的图像向下平移2个单位长度得到的。
(2)用动态几何软件探究:
打开动态几何软件,在$x$轴上任取一点A,用字母$a$表示点A的横坐标,在$y$轴上任取一点K,用字母$k$表示点K的纵坐标。
画二次函数$y = ax^{2}$的图像和$y = ax^{2} + k$的图像。
在$x$轴上任取一点M,过点M画$x$轴的垂线l,直线l分别交二次函数$y = ax^{2}$与$y = ax^{2} + k$的图像于点C、D。
度量并计算点C、D的纵坐标之差,发现这个差值就是$k$,即函数$y = ax^{2} + k$与$y = ax^{2}$的图像在相同$x$值下的$y$值之差。
移动点A、K,改变$a$、$k$的值,再移动点M,观察点C、D的纵坐标之差,发现无论$a$、$k$和$x$如何变化,这个差值始终等于$k$。
思考:二次函数$y = ax^{2} + k$的图像如何由二次函数$y = ax^{2}$的图像平移得到?
答:当$k > 0$时,二次函数$y = ax^{2} + k$的图像由二次函数$y = ax^{2}$的图像向上平移$k$个单位长度得到;当$k < 0$时,二次函数$y = ax^{2} + k$的图像由二次函数$y = ax^{2}$的图像向下平移$|k|$个单位长度得到。
【答案】:
(1) 发现图像沿$y$轴上下平移,计算验证了平移规律;
(2) 发现点C、D的纵坐标之差为$k$,思考得出二次函数$y = ax^{2} + k$的图像由二次函数$y = ax^{2}$的图像平移得到。
查看更多完整答案,请扫码查看


