2025年数学实验手册九年级全一册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年数学实验手册九年级全一册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
2. 覆盖三角形
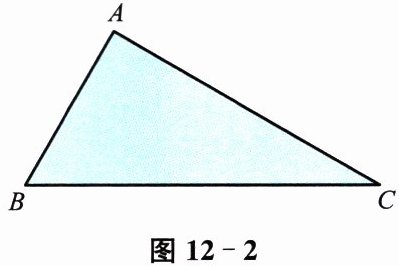
(1)画出图 12-2 中$Rt\triangle ABC$的最小覆盖圆.
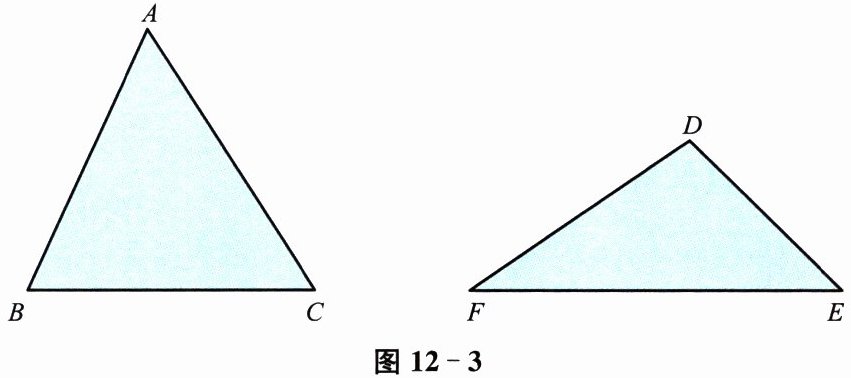
(2)剪下附录 B 中的透明纸片⑥~⑩,分别将这些透明纸片中的圆覆盖在图 12-3 中的$\triangle ABC和\triangle DEF$上,分别找出这两个三角形的最小覆盖圆.
三角形的最小覆盖圆有何特征?请与同伴交流.
(1)画出图 12-2 中$Rt\triangle ABC$的最小覆盖圆.

(2)剪下附录 B 中的透明纸片⑥~⑩,分别将这些透明纸片中的圆覆盖在图 12-3 中的$\triangle ABC和\triangle DEF$上,分别找出这两个三角形的最小覆盖圆.

三角形的最小覆盖圆有何特征?请与同伴交流.
答案:
(1) 解:作Rt△ABC斜边BC的中点O,以O为圆心,BC长的一半为半径画圆,该圆即为Rt△ABC的最小覆盖圆。
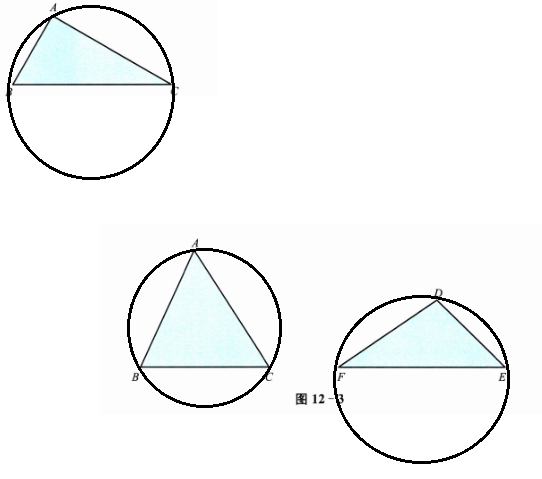
(2) 解:△ABC的最小覆盖圆是以其外接圆为最小覆盖圆;△DEF的最小覆盖圆是以其最长边为直径的圆。
三角形最小覆盖圆的特征:锐角三角形的最小覆盖圆是其外接圆;直角三角形的最小覆盖圆是以斜边为直径的圆;钝角三角形的最小覆盖圆是以最长边为直径的圆。
(1) 解:作Rt△ABC斜边BC的中点O,以O为圆心,BC长的一半为半径画圆,该圆即为Rt△ABC的最小覆盖圆。
(2) 解:△ABC的最小覆盖圆是以其外接圆为最小覆盖圆;△DEF的最小覆盖圆是以其最长边为直径的圆。
三角形最小覆盖圆的特征:锐角三角形的最小覆盖圆是其外接圆;直角三角形的最小覆盖圆是以斜边为直径的圆;钝角三角形的最小覆盖圆是以最长边为直径的圆。

3. 画四边形的最小覆盖圆
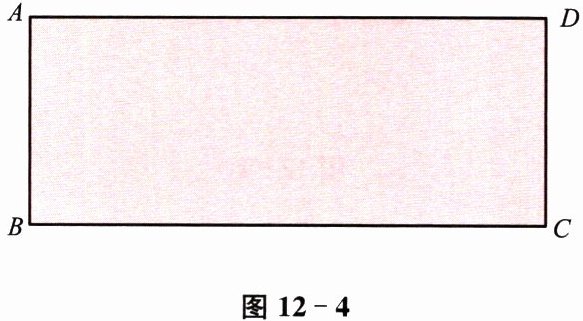
(1)画出图 12-4 中矩形 ABCD 的最小覆盖圆. 与同伴交流画图的过程.
如图 12-5,在矩形 ABCD 中,$AB= 2\ cm$,$BC= 4\ cm$. 若两个等圆完全覆盖这个矩形,请求出这样的两个等圆的最小半径.
(1)画出图 12-4 中矩形 ABCD 的最小覆盖圆. 与同伴交流画图的过程.

如图 12-5,在矩形 ABCD 中,$AB= 2\ cm$,$BC= 4\ cm$. 若两个等圆完全覆盖这个矩形,请求出这样的两个等圆的最小半径.

答案:
(1) 解:
(2) 解:设矩形ABCD中,AB=2cm,BC=4cm,取AD中点E,BC中点F,连接EF,EF中点为O。设两个等圆圆心分别为O₁、O₂,在EF上且O₁O₂=2r。O₁到A、B距离为r,O₂到C、D距离为r。设O₁E=x,则O₁F=4 - x,O₂E=4 - x,O₂F=x。在Rt△AO₁E中,AE=1cm,OE=x,由勾股定理得r² = 1² + x²;在Rt△CO₂F中,CF=1cm,OF=x,同理r² = 1² + x²。又O₁O₂=2r=4 - 2x,联立得2r=4 - 2x,x=2 - r,代入r²=1 + (2 - r)²,解得r=5/4。
答:两个等圆的最小半径为5/4 cm。
(1) 解:
(2) 解:设矩形ABCD中,AB=2cm,BC=4cm,取AD中点E,BC中点F,连接EF,EF中点为O。设两个等圆圆心分别为O₁、O₂,在EF上且O₁O₂=2r。O₁到A、B距离为r,O₂到C、D距离为r。设O₁E=x,则O₁F=4 - x,O₂E=4 - x,O₂F=x。在Rt△AO₁E中,AE=1cm,OE=x,由勾股定理得r² = 1² + x²;在Rt△CO₂F中,CF=1cm,OF=x,同理r² = 1² + x²。又O₁O₂=2r=4 - 2x,联立得2r=4 - 2x,x=2 - r,代入r²=1 + (2 - r)²,解得r=5/4。
答:两个等圆的最小半径为5/4 cm。
查看更多完整答案,请扫码查看


