第63页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
8. (2024·呼和浩特)如图,正四边形ABCD和正五边形CEFGH内接于⊙O,AD和EF相交于点M,则∠AMF的度数为______。
]
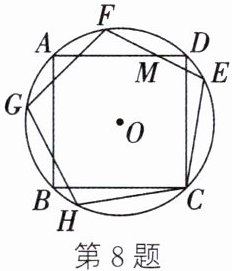
]

答案:
27° 解析:如图,连接OG、OF、OD、OE、DF、AC.$\because$ 四边形ABCD是正方形,$\therefore \angle ADC=90^\circ$,$\therefore$ AC过圆心O,$\therefore \angle AOD=\frac{1}{4}× 360^\circ=90^\circ$,$\angle FOG=\angle EOF=\frac{1}{5}× 360^\circ=7 2^\circ$.$\because$ 正五边形CEFGH内接于$\odot O$,$\therefore \widehat{GH}=\widehat{CH}=\widehat{FE}=\widehat{CE}$,$\therefore \widehat{GC}=\widehat{FC}$,$\therefore \angle GOC=\angle FOC$,$\therefore \angle AOG=\angle AOF=\frac{1}{2}\angle FOG=36^\circ$,$\therefore \angle DOF=90^\circ - 36^\circ=54^\circ$,$\therefore \angle DOE=72^\circ - 54^\circ=18^\circ$$\therefore \angle AMF=\angle MFD+\angle MDF=\frac{1}{2}\angle DOE+\frac{ 1}{2}\angle AOF=\frac{1}{2}× 18^\circ+\frac{1}{2}× 36^\circ=27^\circ$.
27° 解析:如图,连接OG、OF、OD、OE、DF、AC.$\because$ 四边形ABCD是正方形,$\therefore \angle ADC=90^\circ$,$\therefore$ AC过圆心O,$\therefore \angle AOD=\frac{1}{4}× 360^\circ=90^\circ$,$\angle FOG=\angle EOF=\frac{1}{5}× 360^\circ=7 2^\circ$.$\because$ 正五边形CEFGH内接于$\odot O$,$\therefore \widehat{GH}=\widehat{CH}=\widehat{FE}=\widehat{CE}$,$\therefore \widehat{GC}=\widehat{FC}$,$\therefore \angle GOC=\angle FOC$,$\therefore \angle AOG=\angle AOF=\frac{1}{2}\angle FOG=36^\circ$,$\therefore \angle DOF=90^\circ - 36^\circ=54^\circ$,$\therefore \angle DOE=72^\circ - 54^\circ=18^\circ$$\therefore \angle AMF=\angle MFD+\angle MDF=\frac{1}{2}\angle DOE+\frac{ 1}{2}\angle AOF=\frac{1}{2}× 18^\circ+\frac{1}{2}× 36^\circ=27^\circ$.

9. (2024·雅安)如图,⊙O的周长为8π,正六边形ABCDEF内接于⊙O,则△OAB的面积为
$4\sqrt{3}$
。
答案:
【解析】:
本题考查正多边形和圆的关系。
正六边形内接于圆,意味着正六边形的六个顶点都在圆上。
连接圆心$O$与正六边形的各个顶点,
可以得到六个等腰三角形,
即$\triangle OAB$,$\triangle OBC$,$\triangle OCD$,$\triangle ODE$,$\triangle OEF$,$\triangle OFA$。
由于正六边形的对称性,这六个等腰三角形都是全等的。
圆的周长公式为$C = 2\pi r$。
根据题目,圆的周长为$8\pi$,则有$2\pi r = 8\pi$,
解得$r = 4$。
由于正六边形的对称性,圆心角$\angle AOB$为$360^\circ ÷ 6 = 60^\circ$。
在等腰三角形$\triangle OAB$中,$OA = OB = r = 4$,且$\angle AOB = 60^\circ$。
过点$O$作$OG \perp AB$于点$G$,
则$\angle AOG = \angle BOG = 30^\circ$(等腰三角形三线合一)。
利用三角函数或者特殊角三角形的性质,
我们可以得到$OG = OA × \cos 30^\circ = 4 × \frac{\sqrt{3}}{2} = 2\sqrt{3}$,
$AG=OA × \sin 30^\circ = 4 × \frac{1}{2} = 2$,
所以$AB=2AG=4$。
所以$\triangle OAB$的面积为$\frac{1}{2} × AB × OG = \frac{1}{2} × 4 × 2\sqrt{3} = 4\sqrt{3}$。
【答案】:
$4\sqrt{3}$
本题考查正多边形和圆的关系。
正六边形内接于圆,意味着正六边形的六个顶点都在圆上。
连接圆心$O$与正六边形的各个顶点,
可以得到六个等腰三角形,
即$\triangle OAB$,$\triangle OBC$,$\triangle OCD$,$\triangle ODE$,$\triangle OEF$,$\triangle OFA$。
由于正六边形的对称性,这六个等腰三角形都是全等的。
圆的周长公式为$C = 2\pi r$。
根据题目,圆的周长为$8\pi$,则有$2\pi r = 8\pi$,
解得$r = 4$。
由于正六边形的对称性,圆心角$\angle AOB$为$360^\circ ÷ 6 = 60^\circ$。
在等腰三角形$\triangle OAB$中,$OA = OB = r = 4$,且$\angle AOB = 60^\circ$。
过点$O$作$OG \perp AB$于点$G$,
则$\angle AOG = \angle BOG = 30^\circ$(等腰三角形三线合一)。
利用三角函数或者特殊角三角形的性质,
我们可以得到$OG = OA × \cos 30^\circ = 4 × \frac{\sqrt{3}}{2} = 2\sqrt{3}$,
$AG=OA × \sin 30^\circ = 4 × \frac{1}{2} = 2$,
所以$AB=2AG=4$。
所以$\triangle OAB$的面积为$\frac{1}{2} × AB × OG = \frac{1}{2} × 4 × 2\sqrt{3} = 4\sqrt{3}$。
【答案】:
$4\sqrt{3}$
10. (新考向·数学文化)如图,第29届自贡国际恐龙灯会“辉煌新时代”主题灯组上有一幅不完整的正多边形图案,小华量得图中一边与对角线的夹角∠ACB= 15°,算出这个正多边形的边数为______。
]
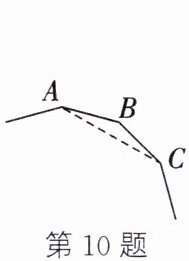
]

12
答案:
1. 首先,设这个正多边形的边数为$n$:
因为多边形内角和公式为$(n - 2)×180^{\circ}$,且正多边形每个内角都相等。
由图可知$\angle BAC=\angle ACB = 15^{\circ}$(等腰三角形两底角相等,正多边形的边相等,$AB = BC$)。
根据三角形外角性质,正多边形的一个内角$\angle ABC=180^{\circ}-2×15^{\circ}=150^{\circ}$。
2. 然后,根据正多边形内角公式$\frac{(n - 2)×180^{\circ}}{n}$:
令$\frac{(n - 2)×180^{\circ}}{n}=150^{\circ}$。
方程两边同时乘以$n$得:$(n - 2)×180 = 150n$。
展开括号:$180n-360 = 150n$。
移项得:$180n-150n = 360$。
合并同类项:$30n = 360$。
解得$n = 12$。
所以这个正多边形的边数为$12$。
因为多边形内角和公式为$(n - 2)×180^{\circ}$,且正多边形每个内角都相等。
由图可知$\angle BAC=\angle ACB = 15^{\circ}$(等腰三角形两底角相等,正多边形的边相等,$AB = BC$)。
根据三角形外角性质,正多边形的一个内角$\angle ABC=180^{\circ}-2×15^{\circ}=150^{\circ}$。
2. 然后,根据正多边形内角公式$\frac{(n - 2)×180^{\circ}}{n}$:
令$\frac{(n - 2)×180^{\circ}}{n}=150^{\circ}$。
方程两边同时乘以$n$得:$(n - 2)×180 = 150n$。
展开括号:$180n-360 = 150n$。
移项得:$180n-150n = 360$。
合并同类项:$30n = 360$。
解得$n = 12$。
所以这个正多边形的边数为$12$。
11. 如图,正五边形ABCDE内接于⊙O,先作直径AF;再以点F为圆心,FO为半径作圆弧,与⊙O交于点M、N;最后连接AM、MN、NA。
(1) 求∠ABC的度数。
(2) △AMN是正三角形吗?请说明理由。
(3) 从点A开始,以DN为半径,在⊙O上依次截取点,再依次连接这些分点,得到正n边形,求n的值。
]
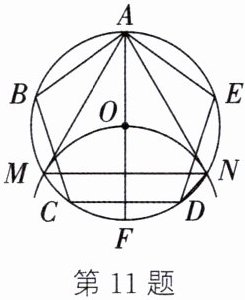
(1) 求∠ABC的度数。
(2) △AMN是正三角形吗?请说明理由。
(3) 从点A开始,以DN为半径,在⊙O上依次截取点,再依次连接这些分点,得到正n边形,求n的值。
]

答案:
(1)解:
∵ABCDE是正五边形,
∴∠ABC=(5-2)×180°/5=108°。
(2)解:△AMN是正三角形,理由如下:
设⊙O半径为r,则FO=r,FM=FO=r,
∵OM=r,
∴△OMF是等边三角形,∠MOF=60°,
同理∠NOF=60°,
∴∠MON=120°,
∵AF是直径,
∴∠AOF=180°,
∴∠AOM=∠AOF - ∠MOF=120°,∠AON=∠AOF + ∠NOF=240°,
∴弧AM度数为120°,弧AN度数为240°,弧MN度数为120°,
∴弧AM=弧MN=弧NA,
∴AM=MN=NA,即△AMN是正三角形。
(3)解:连接OD、ON、DN,设⊙O半径为r,
由
(2)知∠NOF=60°,正五边形ABCDE中,∠DOF=360°/5=72°,
∴∠DON=∠DOF + ∠NOF=132°,
在△DON中,由余弦定理得:
DN²=OD² + ON² - 2·OD·ON·cos∠DON=2r² - 2r²cos132°=2r²(1 - cos132°),
设⊙O上正n边形边长为DN,则边长²=2r²(1 - cos(360°/n)),
∴2r²(1 - cos(360°/n))=2r²(1 - cos132°),
∴cos(360°/n)=cos132°,
∵360°/n为正多边形中心角,0°<360°/n<180°,
∴360°/n=132°,解得n=30/11(舍去)或360°/n=360° - 132°=228°(舍去),
或由弧DN度数=∠DON=132°,圆周长对应360°,
n=360°/(弧DN度数对应的中心角),
∵DN为正n边形边长,其中心角为360°/n,
又弧DN度数=132°,则360°/n=12°(132°=11×12°,360°=30×12°),
∴n=30。
(1)解:
∵ABCDE是正五边形,
∴∠ABC=(5-2)×180°/5=108°。
(2)解:△AMN是正三角形,理由如下:
设⊙O半径为r,则FO=r,FM=FO=r,
∵OM=r,
∴△OMF是等边三角形,∠MOF=60°,
同理∠NOF=60°,
∴∠MON=120°,
∵AF是直径,
∴∠AOF=180°,
∴∠AOM=∠AOF - ∠MOF=120°,∠AON=∠AOF + ∠NOF=240°,
∴弧AM度数为120°,弧AN度数为240°,弧MN度数为120°,
∴弧AM=弧MN=弧NA,
∴AM=MN=NA,即△AMN是正三角形。
(3)解:连接OD、ON、DN,设⊙O半径为r,
由
(2)知∠NOF=60°,正五边形ABCDE中,∠DOF=360°/5=72°,
∴∠DON=∠DOF + ∠NOF=132°,
在△DON中,由余弦定理得:
DN²=OD² + ON² - 2·OD·ON·cos∠DON=2r² - 2r²cos132°=2r²(1 - cos132°),
设⊙O上正n边形边长为DN,则边长²=2r²(1 - cos(360°/n)),
∴2r²(1 - cos(360°/n))=2r²(1 - cos132°),
∴cos(360°/n)=cos132°,
∵360°/n为正多边形中心角,0°<360°/n<180°,
∴360°/n=132°,解得n=30/11(舍去)或360°/n=360° - 132°=228°(舍去),
或由弧DN度数=∠DON=132°,圆周长对应360°,
n=360°/(弧DN度数对应的中心角),
∵DN为正n边形边长,其中心角为360°/n,
又弧DN度数=132°,则360°/n=12°(132°=11×12°,360°=30×12°),
∴n=30。
12. 如图,在等边三角形ABC中,E、F、G、H、L、K分别是各边的三等分点。
(1) 求证:六边形EFGHLK是正六边形;
(2) 若AB= 3cm,求正六边形EFGHLK的面积。
]
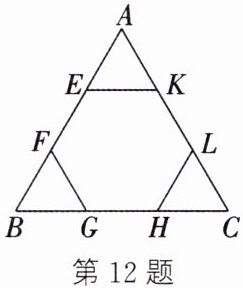
(1) 求证:六边形EFGHLK是正六边形;
(2) 若AB= 3cm,求正六边形EFGHLK的面积。
]

答案:
1. (1)证明:
因为$\triangle ABC$是等边三角形,$AB = BC = AC$,$\angle A=\angle B=\angle C = 60^{\circ}$。
又因为$E$、$F$、$G$、$H$、$L$、$K$分别是各边的三等分点,所以$AE=\frac{1}{3}AB$,$AF=\frac{2}{3}AB$,$BF=\frac{1}{3}AB$,$BG=\frac{2}{3}BC$,$CH=\frac{1}{3}BC$,$CL=\frac{2}{3}AC$,$AK=\frac{1}{3}AC$。
在$\triangle AEK$中,$AE = AK=\frac{1}{3}AB$,$\angle A = 60^{\circ}$,根据等边三角形的判定(有一个角是$60^{\circ}$的等腰三角形是等边三角形),可得$\triangle AEK$是等边三角形,所以$EK=\frac{1}{3}AB$,$\angle AEK=\angle AKE = 60^{\circ}$。
同理可得$\triangle BFG$,$\triangle CHL$都是等边三角形,$FG=\frac{1}{3}AB$,$\angle BFG=\angle BGF = 60^{\circ}$,$HL=\frac{1}{3}AB$,$\angle CHL=\angle CLH = 60^{\circ}$。
因为$EF=\frac{1}{3}AB$,$GH=\frac{1}{3}AB$,$LK=\frac{1}{3}AB$,且$\angle FEK=\angle EFG=\angle FGH=\angle GHL=\angle HLK=\angle LKE = 120^{\circ}$。
所以$EF = FG=GH = HL=LK = EK$,且六个内角都相等。
所以六边形$EFGHLK$是正六边形。
2. (2)
已知$AB = 3cm$,则$S_{\triangle ABC}=\frac{\sqrt{3}}{4}AB^{2}=\frac{\sqrt{3}}{4}×3^{2}=\frac{9\sqrt{3}}{4}(cm^{2})$。
由(1)可知$\triangle AEK$,$\triangle BFG$,$\triangle CHL$都是等边三角形,且边长为$1cm$。
$S_{\triangle AEK}=S_{\triangle BFG}=S_{\triangle CHL}=\frac{\sqrt{3}}{4}×1^{2}=\frac{\sqrt{3}}{4}(cm^{2})$。
正六边形$EFGHLK$的面积$S = S_{\triangle ABC}-3S_{\triangle AEK}$。
把$S_{\triangle ABC}=\frac{9\sqrt{3}}{4}$,$S_{\triangle AEK}=\frac{\sqrt{3}}{4}$代入可得:
$S=\frac{9\sqrt{3}}{4}-3×\frac{\sqrt{3}}{4}=\frac{9\sqrt{3}-3\sqrt{3}}{4}=\frac{6\sqrt{3}}{4}=\frac{3\sqrt{3}}{2}(cm^{2})$。
综上,(1)证明如上;(2)正六边形$EFGHLK$的面积是$\frac{3\sqrt{3}}{2}cm^{2}$。
因为$\triangle ABC$是等边三角形,$AB = BC = AC$,$\angle A=\angle B=\angle C = 60^{\circ}$。
又因为$E$、$F$、$G$、$H$、$L$、$K$分别是各边的三等分点,所以$AE=\frac{1}{3}AB$,$AF=\frac{2}{3}AB$,$BF=\frac{1}{3}AB$,$BG=\frac{2}{3}BC$,$CH=\frac{1}{3}BC$,$CL=\frac{2}{3}AC$,$AK=\frac{1}{3}AC$。
在$\triangle AEK$中,$AE = AK=\frac{1}{3}AB$,$\angle A = 60^{\circ}$,根据等边三角形的判定(有一个角是$60^{\circ}$的等腰三角形是等边三角形),可得$\triangle AEK$是等边三角形,所以$EK=\frac{1}{3}AB$,$\angle AEK=\angle AKE = 60^{\circ}$。
同理可得$\triangle BFG$,$\triangle CHL$都是等边三角形,$FG=\frac{1}{3}AB$,$\angle BFG=\angle BGF = 60^{\circ}$,$HL=\frac{1}{3}AB$,$\angle CHL=\angle CLH = 60^{\circ}$。
因为$EF=\frac{1}{3}AB$,$GH=\frac{1}{3}AB$,$LK=\frac{1}{3}AB$,且$\angle FEK=\angle EFG=\angle FGH=\angle GHL=\angle HLK=\angle LKE = 120^{\circ}$。
所以$EF = FG=GH = HL=LK = EK$,且六个内角都相等。
所以六边形$EFGHLK$是正六边形。
2. (2)
已知$AB = 3cm$,则$S_{\triangle ABC}=\frac{\sqrt{3}}{4}AB^{2}=\frac{\sqrt{3}}{4}×3^{2}=\frac{9\sqrt{3}}{4}(cm^{2})$。
由(1)可知$\triangle AEK$,$\triangle BFG$,$\triangle CHL$都是等边三角形,且边长为$1cm$。
$S_{\triangle AEK}=S_{\triangle BFG}=S_{\triangle CHL}=\frac{\sqrt{3}}{4}×1^{2}=\frac{\sqrt{3}}{4}(cm^{2})$。
正六边形$EFGHLK$的面积$S = S_{\triangle ABC}-3S_{\triangle AEK}$。
把$S_{\triangle ABC}=\frac{9\sqrt{3}}{4}$,$S_{\triangle AEK}=\frac{\sqrt{3}}{4}$代入可得:
$S=\frac{9\sqrt{3}}{4}-3×\frac{\sqrt{3}}{4}=\frac{9\sqrt{3}-3\sqrt{3}}{4}=\frac{6\sqrt{3}}{4}=\frac{3\sqrt{3}}{2}(cm^{2})$。
综上,(1)证明如上;(2)正六边形$EFGHLK$的面积是$\frac{3\sqrt{3}}{2}cm^{2}$。
查看更多完整答案,请扫码查看


