《2025年通成学典课时作业本九年级数学上册苏科版宿迁专版》

8. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC。若∠CAB= 22.5°,CD= 8cm,则⊙O的半径为$4\sqrt{2}$cm。

答案： $4\sqrt{2}$

9. 如图,在⊙O中,$\overset{\frown}{AB}= 2\overset{\frown}{AC}$,AD⊥OC于点D。若AB= 8,则AD的长为______4。

答案： 4

10. 如图,AB是⊙O的直径,AC是⊙O的弦,OD⊥AC于点D,DO的延长线交⊙O于点E。若AC= $4\sqrt{2}$,DE= 4,则BC的长为______2。

答案： 2

11. (2024·宿城段考)如图,⊙O的直径为10,弦AB的长为8,M是弦AB上的动点,则OM长的取值范围是$3 \leqslant OM \leqslant 5$。

答案： $3 \leqslant OM \leqslant 5$

12. 如图,在Rt△ABC中,∠C= 90°,以点C为圆心、AC为半径的⊙C与AB相交于点D。若AC= 6,BC= 8,则AD的长为______。

答案：
$\frac{36}{5}$ 解析:如图，连接 CD,过点 C 作 $CH \perp AB$ 于点 H,则 $AH=\frac{1}{2}AD$.在 $Rt\triangle ABC$ 中,由勾股定理,得 $AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{6^{2}+8^{2}}=10$.由 $S_{\triangle ABC}=\frac{1}{2}AC \cdot BC=\frac{1}{2}AB \cdot CH$,即 $\frac{1}{2}× 6× 8=\frac{1}{2}× 10\cdot CH$,得 $CH=\frac{24}{5}$.在 $Rt\triangle AHC$ 中,由勾股定理,得 $AH=\sqrt{AC^{2}-CH^{2}}=\sqrt{6^{2}-(\frac{24}{5})^{2}}=\frac{18}{5}$.
∴ $AD=2AH=\frac{36}{5}$.

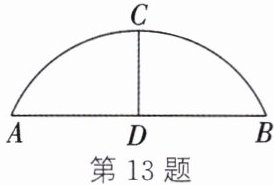
13. (新情境·现实生活)(2023·沭阳段考)如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m。
(1)求拱桥的半径；
(2)有一艘宽为5m的货船,船舱顶部为矩形,并高出水面3.6m,此货船是否能顺利通过这座拱桥(参考数据：$\sqrt{5.04}\approx2.245$)?

答案：
（1）如图，设该圆弧的圆心为 O,连接 OB、OD.根据题意，得 O、D、C 三点共线，且 $OC \perp AB$,则 D 为 AB 的中点.
∵ $AB = 12m$,
∴ $BD=\frac{1}{2}AB = 6m$.设 $OB = OC = r m$.
∵ $CD = 4m$,
∴ $OD=(r - 4)m$.在 $Rt\triangle BOD$ 中,根据勾股定理,得 $BO^{2}=OD^{2}+BD^{2}$,即 $r^{2}=(r - 4)^{2}+6^{2}$,解得 $r = 6.5$,即拱桥的半径为 $6.5m$ （2）在 DC 上取 $DE = 3.6m$,过点 E 作 $MN // AB$ 交 $\overset{\frown}{AC}$ 于点 M,交 $\overset{\frown}{BC}$ 于点 N,连接 ON.
∵ $CD = 4m$,船舱顶部为矩形,并高出水面 $3.6m$,
∴ $CE = CD - DE = 4 - 3.6 = 0.4(m)$,
∴ $OE = OC - CE = 6.5 - 0.4 = 6.1(m)$.在 $Rt\triangle OEN$ 中,根据勾股定理,得 $EN^{2}=ON^{2}-OE^{2}=6.5^{2}-6.1^{2}=5.04$,
∴ $EN=\sqrt{5.04}m$,
∴ $MN = 2EN = 2× \sqrt{5.04}\approx 4.49(m)＜5m$,
∴ 此货船不能顺利通过这座拱桥

14. (2024·包头)如图,AB是⊙O的直径,BC、BD是⊙O的两条弦,点C与点D在AB的两侧,E是OB上一点(OE＞BE),连接OC、CE。若∠BOC= 2∠BCE,且BD= 2OE,求证：BD//OC。

答案：
如图，过点 O 分别作 $OH \perp BC$、$OK \perp BD$,垂足依次为 H、K.
∵ $OK \perp BD$,OK 经过圆心,
∴ $\angle OKB = 90^{\circ}$,$BD = 2BK$.
∵ $BD = 2OE$,
∴ $OE = BK$.
∵ $OB = OC$,$OH \perp BC$,
∴ $\angle BOC = 2\angle BOH$,$\angle OHB = 90^{\circ}$,
∴ 在 $Rt\triangle OHB$ 中,$\angle BOH+\angle OBH = 90^{\circ}$.
∵ $\angle BOC = 2\angle BCE$,
∴ $\angle BOH=\angle BCE$,
∴ $\angle BCE+\angle OBH = 90^{\circ}$,
∴ $\angle OEC=\angle BCE+\angle OBH = 90^{\circ}$.在 $Rt\triangle OEC$ 和 $Rt\triangle BKO$ 中,$\left\{\begin{array}{l} OC = BO\\ OE = BK\end{array}\right.$,
∴ $Rt\triangle OEC \cong Rt\triangle BKO$,
∴ $\angle COE=\angle OBK$,
∴ $BD // OC$