1. 在修建高速公路时,有时需要将弯曲的道路改直,依据是(
A.两点之间线段最短
B.两点确定一条直线
C.线段有两个端点
D.线段可以比较大小
A
)。A.两点之间线段最短
B.两点确定一条直线
C.线段有两个端点
D.线段可以比较大小
答案:
A
2. 如图所示的四条线段 $ a,b,c,d $ 按照长短顺序排列应该是(
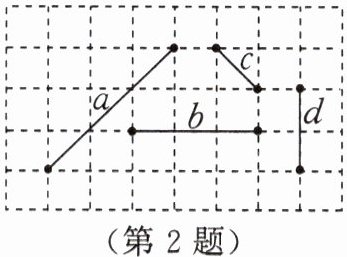
A.$ a > b > c > d $
B.$ a > b > d > c $
C.$ a > d > c > b $
D.$ a > d > b > c $
B
)。
A.$ a > b > c > d $
B.$ a > b > d > c $
C.$ a > d > c > b $
D.$ a > d > b > c $
答案:
B
3. 如图,延长线段 $ AB $ 到 $ C $,使 $ BC = 4 $。若 $ AB = 8 $,则线段 $ AC $ 的长是 $ BC $ 长的
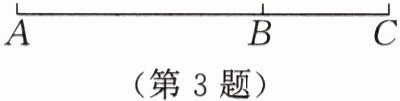
3倍
。
答案:
3倍
4. 如图,已知点 $ D $ 是 $ AB $ 的中点,点 $ E $ 是 $ BC $ 的中点。若 $ AC = 8 $,$ EC = 3 $,则 $ AD = $

1
。
答案:
1
5. 如图,已知线段 $ a,b $,求作线段 $ AB = 2a + b $。


答案:
解:如图。
(1)作射线AM;
(2)在AM上顺次截取AB₁=a,B₁B₂=a,B₂B=b,则线段AB=2a+b。
解:如图。
(1)作射线AM;
(2)在AM上顺次截取AB₁=a,B₁B₂=a,B₂B=b,则线段AB=2a+b。

6. 如图,要在直线 $ PQ $ 上找一点 $ C $,使 $ PC = 3CQ $,则点 $ C $ 应在(
A.$ P,Q $ 之间
B.点 $ P $ 的左边
C.点 $ Q $ 的右边
D.$ P,Q $ 之间或点 $ Q $ 的右边
D
)。
A.$ P,Q $ 之间
B.点 $ P $ 的左边
C.点 $ Q $ 的右边
D.$ P,Q $ 之间或点 $ Q $ 的右边
答案:
D
7. 若 $ A,B,C $ 三点在同一直线上,且线段 $ AB = 4 \mathrm{cm} $,$ BC = 2 \mathrm{cm} $,则 $ A,C $ 两点之间的距离为(
A.$ 2 \mathrm{cm} $
B.$ 6 \mathrm{cm} $
C.$ 2 \mathrm{cm} $ 或 $ 6 \mathrm{cm} $
D.无法确定
C
)。A.$ 2 \mathrm{cm} $
B.$ 6 \mathrm{cm} $
C.$ 2 \mathrm{cm} $ 或 $ 6 \mathrm{cm} $
D.无法确定
答案:
C
8. 已知 $ A,B,C $ 三点在同一条直线上,点 $ M,N $ 分别为线段 $ AB,BC $ 的中点,且 $ AB = 50 $,$ BC = 20 $,求 $ MN $ 的长。
答案:
解:因为点M,N分别为AB,BC的中点,所以BM=$\frac{1}{2}$AB=25,BN=$\frac{1}{2}$BC=10。如图①,MN=BM+BN=25+10=35;如图②,MN=BM−BN=25−10=15。综上,MN的长为35或15。
解:因为点M,N分别为AB,BC的中点,所以BM=$\frac{1}{2}$AB=25,BN=$\frac{1}{2}$BC=10。如图①,MN=BM+BN=25+10=35;如图②,MN=BM−BN=25−10=15。综上,MN的长为35或15。

9. 【综合与实践】如图,$ A,B,C $ 是一条公路上的三个村庄,$ A,B $ 间的路程为 $ 100 \mathrm{km} $,$ A,C $ 间的路程为 $ 40 \mathrm{km} $。现计划在 $ A,B $ 之间建一个车站 $ P $,设 $ P,C $ 之间的路程为 $ x \mathrm{km} $。
(1) 用含 $ x $ 的代数式表示车站到三个村庄的路程之和。
(2) 若路程之和为 $ 102 \mathrm{km} $,则车站应建在何处?
(3) 若要使车站到三个村庄的路程总和最小,则车站应建在何处?路程总和的最小值是多少?

(1) 用含 $ x $ 的代数式表示车站到三个村庄的路程之和。
(2) 若路程之和为 $ 102 \mathrm{km} $,则车站应建在何处?
(3) 若要使车站到三个村庄的路程总和最小,则车站应建在何处?路程总和的最小值是多少?

答案:
解:
(1)路程之和为PA+PB+PC=AB+PC=(100+x)km。
(2)因为100+x=102,所以x=2,所以车站应建在C左侧或右侧2km处。
(3)当x=0时,x+100=100,所以要使车站到三个村庄的路程总和最小,车站应建在C处,且路程总和的最小值为100km。
(1)路程之和为PA+PB+PC=AB+PC=(100+x)km。
(2)因为100+x=102,所以x=2,所以车站应建在C左侧或右侧2km处。
(3)当x=0时,x+100=100,所以要使车站到三个村庄的路程总和最小,车站应建在C处,且路程总和的最小值为100km。
查看更多完整答案,请扫码查看


