《2025年课堂精练七年级数学上册北师大版福建专版》

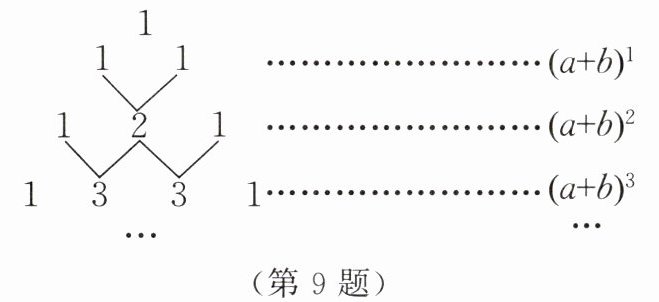
9. 【数学文化】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一个。如图,这个三角形的构造法则是：两腰上的数都是 1,其余每个数均为其上方左右两数之和,它给出了 $ ( a + b ) ^ { n } $($ n $ 为正整数)的展开式(按 $ a $ 的次数由大到小的顺序排列)中各项的系数规律。例如,在三角形中第三行的三个数 1,2,1,恰好对应着 $ ( a + b ) ^ { 2 } $ 的展开式中各项的系数；第四行的四个数 1,3,3,1,恰好对应着 $ ( a + b ) ^ { 3 } $ 的展开式中各项的系数。
(1)根据上面的规律,写出 $ ( a + b ) ^ { 5 } $ 的展开式；
(2)利用(1)的规律计算：$ 2 ^ { 5 } - 5 × 2 ^ { 4 } + 10 × 2 ^ { 3 } - 10 × 2 ^ { 2 } + 5 × 2 - 1 $。

答案：
(1)(a+b)⁵=a⁵+5a⁴b+10a³b²+10a²b³+5ab⁴+b⁵。
(2)2⁵-5×2⁴+10×2³-10×2²+5×2-1=(2-1)⁵=1。

1. 一组按规律排列的多项式：$a + b$,$a^{2}-b^{3}$,$a^{3}+b^{5}$,$a^{4}-b^{7}$,…$$,其中第10个式子是(B)。
A.$a^{10}+b^{19}$
B.$a^{10}-b^{19}$
C.$a^{10}-b^{17}$
D.$a^{10}-b^{21}$

答案： B

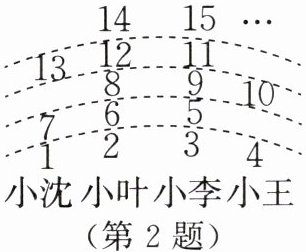
2. 四个小朋友站成一排,老师按图中的规则数数,数到107时对应的小朋友可得一朵红花,那么得红花的小朋友是(C)。

A.小沈
B.小叶
C.小李
D.小王

答案： C

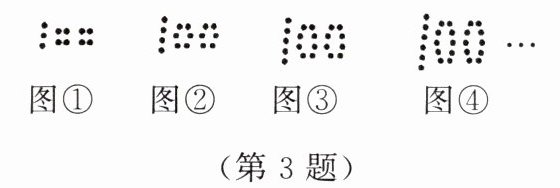
3. 某同学用棋子按照某种规律摆成如图所示的“100”字样。图①有11个棋子,图②有16个棋子,图③有21个棋子,图④有26个棋子,按这种规律,则第20个“100”字样的棋子个数是(C)。


A.125
B.110
C.106
D.101

答案： C

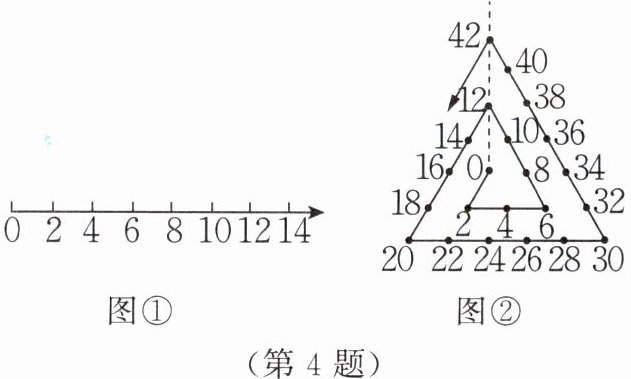
4. 图①是一根起点为0且标有单位长度的射线,现将它弯折成如图②所示的图形,弯折后落在虚线上的点,从下往上第一个数是0,第二个数是12,第三个数是42……$$依此规律,落在虚线上的第五个点对应的数是(D)。

A.90
B.96
C.150
D.156

答案： D