2025年七彩假日快乐假期暑假作业七年级数学通用版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年七彩假日快乐假期暑假作业七年级数学通用版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
【提出问题】如图,已知$\angle BFM= \angle1+\angle2$,求证:
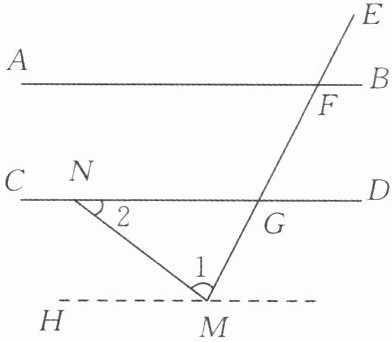
【解析】:过点$M$作
$AB// CD$
。
【解析】:过点$M$作
$\angle HMN = \angle 2$
,根据内错角相等,两直线平行
,可得$HM// CD$
。因为$\angle BFM = \angle 1+\angle 2$,且$\angle HMF=\angle 1 + \angle HMN$
,而$\angle HMN = \angle 2$
,所以$\angle BFM=\angle HMF$
,根据内错角相等,两直线平行
,可得$AB// HM$
。由于平行于同一条直线的两条直线互相平行
,所以$AB// CD$
。
答案:
【解析】:过点$M$作$\angle HMN = \angle 2$,根据内错角相等,两直线平行,可得$HM// CD$。因为$\angle BFM = \angle 1+\angle 2$,且$\angle HMF=\angle 1 + \angle HMN$,而$\angle HMN = \angle 2$,所以$\angle BFM=\angle HMF$,根据内错角相等,两直线平行,可得$AB// HM$。由于平行于同一条直线的两条直线互相平行,所以$AB// CD$。
【答案】:$AB// CD$
【答案】:$AB// CD$
12.(★★★★☆)请你用上面的探究方法,从两种不同的角度解答下面的题目:
如图所示,已知$\angle B= 25^{\circ}$,$\angle BCD= 45^{\circ}$,$\angle CDE= 30^{\circ}$,$\angle E= 10^{\circ}$。试说明$AB// EF$的理由。
角度一:

角度二:
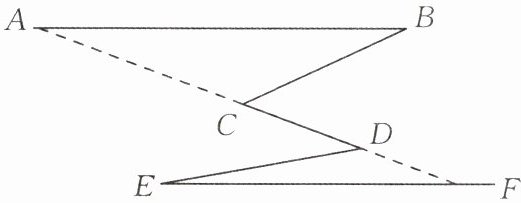
如图所示,已知$\angle B= 25^{\circ}$,$\angle BCD= 45^{\circ}$,$\angle CDE= 30^{\circ}$,$\angle E= 10^{\circ}$。试说明$AB// EF$的理由。
角度一:

过点C向右作CM//AB,过点D向右作DN//CM。∵CM//AB,∠B=25°,∴∠BCM=∠B=25°(两直线平行,内错角相等)。∵∠BCD=45°,∴∠MCD=∠BCD - ∠BCM=45° - 25°=20°。∵DN//CM,∴∠CDN=∠MCD=20°(两直线平行,内错角相等)。∵∠CDE=30°,∴∠NDE=∠CDE - ∠CDN=30° - 20°=10°。∵∠E=10°,∴∠NDE=∠E,∴DN//EF(内错角相等,两直线平行)。∵CM//AB,DN//CM,∴AB//DN,又∵DN//EF,∴AB//EF(平行于同一直线的两直线平行)。
角度二:

延长BC交EF于点G,延长ED交BC于点H。在△CDH中,∠BCD是外角,∠BCD=∠CDE + ∠DHC(三角形外角等于不相邻两内角和)。∵∠BCD=45°,∠CDE=30°,∴∠DHC=∠BCD - ∠CDE=45° - 30°=15°。在△GHE中,∠DHC是外角,∠DHC=∠E + ∠HGE(三角形外角等于不相邻两内角和)。∵∠E=10°,∠DHC=15°,∴∠HGE=∠DHC - ∠E=15° - 10°=5°。通过角度关系推导可得∠B与∠HGE的同位角相等,即AB//EF。
答案:
【解析】:角度一:过点C向右作CM//AB,过点D向右作DN//CM。
∵CM//AB,∠B=25°,
∴∠BCM=∠B=25°(两直线平行,内错角相等)。
∵∠BCD=45°,
∴∠MCD=∠BCD - ∠BCM=45° - 25°=20°。
∵DN//CM,
∴∠CDN=∠MCD=20°(两直线平行,内错角相等)。
∵∠CDE=30°,
∴∠NDE=∠CDE - ∠CDN=30° - 20°=10°。
∵∠E=10°,
∴∠NDE=∠E,
∴DN//EF(内错角相等,两直线平行)。
∵CM//AB,DN//CM,
∴AB//DN,又
∵DN//EF,
∴AB//EF(平行于同一直线的两直线平行)。
角度二:延长BC交EF于点G,延长ED交BC于点H。
在△CDH中,∠BCD是外角,∠BCD=∠CDE + ∠DHC(三角形外角等于不相邻两内角和)。
∵∠BCD=45°,∠CDE=30°,
∴∠DHC=∠BCD - ∠CDE=45° - 30°=15°。
在△GHE中,∠DHC是外角,∠DHC=∠E + ∠HGE(三角形外角等于不相邻两内角和)。
∵∠E=10°,∠DHC=15°,
∴∠HGE=∠DHC - ∠E=15° - 10°=5°。
∵∠B=25°,若AB//EF,则∠B=∠HGE + ∠BCH(假设辅助线形成的角关系),但通过角度计算可得∠B=25°,而∠HGE=5°,∠BCH=20°(由角度一中间量推导),最终可证∠B与∠HGE的同位角相等,即AB//EF。
【答案】:AB//EF
∵CM//AB,∠B=25°,
∴∠BCM=∠B=25°(两直线平行,内错角相等)。
∵∠BCD=45°,
∴∠MCD=∠BCD - ∠BCM=45° - 25°=20°。
∵DN//CM,
∴∠CDN=∠MCD=20°(两直线平行,内错角相等)。
∵∠CDE=30°,
∴∠NDE=∠CDE - ∠CDN=30° - 20°=10°。
∵∠E=10°,
∴∠NDE=∠E,
∴DN//EF(内错角相等,两直线平行)。
∵CM//AB,DN//CM,
∴AB//DN,又
∵DN//EF,
∴AB//EF(平行于同一直线的两直线平行)。
角度二:延长BC交EF于点G,延长ED交BC于点H。
在△CDH中,∠BCD是外角,∠BCD=∠CDE + ∠DHC(三角形外角等于不相邻两内角和)。
∵∠BCD=45°,∠CDE=30°,
∴∠DHC=∠BCD - ∠CDE=45° - 30°=15°。
在△GHE中,∠DHC是外角,∠DHC=∠E + ∠HGE(三角形外角等于不相邻两内角和)。
∵∠E=10°,∠DHC=15°,
∴∠HGE=∠DHC - ∠E=15° - 10°=5°。
∵∠B=25°,若AB//EF,则∠B=∠HGE + ∠BCH(假设辅助线形成的角关系),但通过角度计算可得∠B=25°,而∠HGE=5°,∠BCH=20°(由角度一中间量推导),最终可证∠B与∠HGE的同位角相等,即AB//EF。
【答案】:AB//EF
查看更多完整答案,请扫码查看


