第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
27.(8 分)如图是某公司发布的一款体感平衡“椅车”。它可当椅子坐,也可当电动车行驶。当驾驶者身体前倾时它会前行,身体后仰时就会倒退,而且能做到侧开。这款车的最大承载质量为 80kg,而它自身质量为 5kg,车轮与地面的接触总面积为$25cm^{2}$。请回答下列问题。(g 取 10N/kg)

(1)“椅车”的车轮刻有花纹的作用是______。
(2)“椅车”匀速行驶时受到的摩擦力是总重力的 0.2 倍,则行驶时“椅车”受到的摩擦力最大为多少牛?
(3)当“椅车”处于最大载重时,对地面的压强是多少?

(1)“椅车”的车轮刻有花纹的作用是______。
(2)“椅车”匀速行驶时受到的摩擦力是总重力的 0.2 倍,则行驶时“椅车”受到的摩擦力最大为多少牛?
(3)当“椅车”处于最大载重时,对地面的压强是多少?
答案:
(1)增大摩擦
(2)$G=mg=(80\mathrm{kg}+5\mathrm{kg})× 10\mathrm{N/kg}=850\mathrm{N}$,则$f=0.2G=0.2× 850\mathrm{N}=170\mathrm{N}$。
(3)$F=G=850\mathrm{N}$,$S=25\mathrm{cm}^{2}=0.0025\mathrm{m}^{2}$,则$p=\frac{F}{S}=\frac{850\mathrm{N}}{0.0025\mathrm{m}^{2}}=3.4× 10^{5}\mathrm{Pa}$。
(1)增大摩擦
(2)$G=mg=(80\mathrm{kg}+5\mathrm{kg})× 10\mathrm{N/kg}=850\mathrm{N}$,则$f=0.2G=0.2× 850\mathrm{N}=170\mathrm{N}$。
(3)$F=G=850\mathrm{N}$,$S=25\mathrm{cm}^{2}=0.0025\mathrm{m}^{2}$,则$p=\frac{F}{S}=\frac{850\mathrm{N}}{0.0025\mathrm{m}^{2}}=3.4× 10^{5}\mathrm{Pa}$。
28.(8 分)如图所示,甲、乙两个均匀正方体放在水平地面上,已知甲的密度为$1000kg/m^{3}$,边长是 0.1m。沿水平或竖直方向将甲、乙各切去一半的体积,并将切去的部分叠放在对方剩余部分的上方,甲、乙对地面压强变化如表所示。(g 取 10N/kg)
(1)甲的质量为______kg。
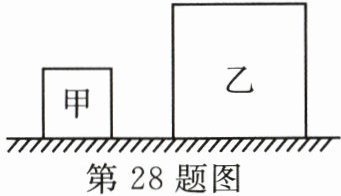
(2)甲是沿______方向切去的。
(3)切掉一半之前,甲对地面的压强是多少帕?
(4)正方体乙的边长为多少厘米?
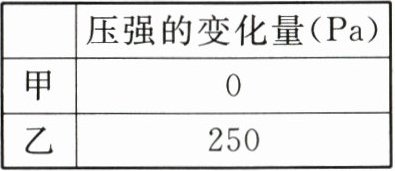
|压强的变化量(Pa)|
|甲 0|
|乙 250|
(1)甲的质量为______kg。

(2)甲是沿______方向切去的。
(3)切掉一半之前,甲对地面的压强是多少帕?
(4)正方体乙的边长为多少厘米?
|压强的变化量(Pa)|
|甲 0|
|乙 250|

答案:
(1)1
(2)水平
(3)因为放在水平面上的物体对地面的压力等于自身重力,则甲对地面的压力为$F_{甲}=G_{甲}$,所以甲对地面的压强$p_{甲}=\frac{F_{甲}}{S_{甲}}=\frac{G_{甲}}{S_{甲}}=\frac{m_{甲}g}{S_{甲}}=\frac{1\mathrm{kg}× 10\mathrm{N/kg}}{(0.1\mathrm{m})^{2}}=1× 10^{3}\mathrm{Pa}$。
(4)由前面解答可知,甲切掉一半体积的质量和乙切割一半体积的质量相等,所以原来甲、乙的质量相等,即$m_{乙}=m_{甲}=1\mathrm{kg}$,切割前乙对地面的压力$F_{乙}=m_{乙}g$,受力面积为$S_{乙}$,当乙沿竖直方向切去一半的体积,并将甲切去一半叠放在乙剩余部分的上方,此时乙对地面压力$F_{乙}'=\frac{1}{2}m_{乙}g+\frac{1}{2}m_{甲}g=m_{乙}g$,受力面积为$\frac{1}{2}S_{乙}$,由表中数据可知,乙的压强的变化量是250Pa,由压强的公式可得乙压强的变化量$\Delta p_{乙}=p_{乙}'-p_{乙}=\frac{m_{乙}g}{\frac{1}{2}S_{乙}}-\frac{m_{乙}g}{S_{乙}}=\frac{m_{乙}g}{S_{乙}}$,则原来乙的底面积$S_{乙}=\frac{m_{乙}g}{\Delta p_{乙}}=\frac{1\mathrm{kg}× 10\mathrm{N/kg}}{250\mathrm{Pa}}=0.04\mathrm{m}^{2}$,故正方体乙的边长$l_{乙}=\sqrt{S_{乙}}=\sqrt{0.04\mathrm{m}^{2}}=0.2\mathrm{m}=20\mathrm{cm}$。
(1)1
(2)水平
(3)因为放在水平面上的物体对地面的压力等于自身重力,则甲对地面的压力为$F_{甲}=G_{甲}$,所以甲对地面的压强$p_{甲}=\frac{F_{甲}}{S_{甲}}=\frac{G_{甲}}{S_{甲}}=\frac{m_{甲}g}{S_{甲}}=\frac{1\mathrm{kg}× 10\mathrm{N/kg}}{(0.1\mathrm{m})^{2}}=1× 10^{3}\mathrm{Pa}$。
(4)由前面解答可知,甲切掉一半体积的质量和乙切割一半体积的质量相等,所以原来甲、乙的质量相等,即$m_{乙}=m_{甲}=1\mathrm{kg}$,切割前乙对地面的压力$F_{乙}=m_{乙}g$,受力面积为$S_{乙}$,当乙沿竖直方向切去一半的体积,并将甲切去一半叠放在乙剩余部分的上方,此时乙对地面压力$F_{乙}'=\frac{1}{2}m_{乙}g+\frac{1}{2}m_{甲}g=m_{乙}g$,受力面积为$\frac{1}{2}S_{乙}$,由表中数据可知,乙的压强的变化量是250Pa,由压强的公式可得乙压强的变化量$\Delta p_{乙}=p_{乙}'-p_{乙}=\frac{m_{乙}g}{\frac{1}{2}S_{乙}}-\frac{m_{乙}g}{S_{乙}}=\frac{m_{乙}g}{S_{乙}}$,则原来乙的底面积$S_{乙}=\frac{m_{乙}g}{\Delta p_{乙}}=\frac{1\mathrm{kg}× 10\mathrm{N/kg}}{250\mathrm{Pa}}=0.04\mathrm{m}^{2}$,故正方体乙的边长$l_{乙}=\sqrt{S_{乙}}=\sqrt{0.04\mathrm{m}^{2}}=0.2\mathrm{m}=20\mathrm{cm}$。
查看更多完整答案,请扫码查看


