《2025年超越训练七年级数学上册人教版四川专版》

14. 已知关于 $x$ 的方程 $(a - 3)x^{|2a - 7|} - 5 = 0$ 是一元一次方程，则 $a$ 的值为.

答案： （此处假设选项中$4$对应的是$B$（由于题目未给选项，按照常规格式假设） ）$B$

15. 用“$\otimes$”定义一种新运算，对于任意有理数 $a$，$b$，$a\otimes b = 5b - 2a$.若 $(3x + 5)\otimes(1 - x) = 1$，则 $x$ 的值为.

答案： $-\frac{6}{11}$。

16. 某商品的进价是 500 元，标价为 750 元，商店要求以利润率不低于 $5\%$ 的售价打折出售，售货员最低可以打折出售此商品.

答案： 7

17. 已知方程 $\frac{1}{6} + 5(x - \frac{1}{2025}) = \frac{1}{3}$，则 $3 + 30(2025x - 1)$ 的值为.

答案： 2028

18. 如图，在三角形 $ABC$ 中，$\angle C = 90^{\circ}$，$BC = 8$ cm，$AC = 6$ cm，$E$ 是 $BC$ 的中点，动点 $P$ 从点 $A$ 出发，先以 2 cm/s 的速度沿 $A→C$ 运动，然后以 1 cm/s 的速度沿 $C→B$ 运动.若设点 $P$ 的运动时间为 $t$ s，当三角形 $APE$ 的面积为 $8$ cm² 时，$t$ 的值为.

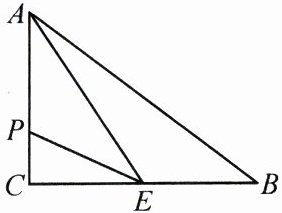
答案：

19. （8 分）解下列方程：
（1）$\frac{5x - 4}{3} - \frac{6x + 21}{5} = 1$；
（2）$x - \frac{1}{2}[x - \frac{1}{2}(x - \frac{1}{2})] = 2$.

答案： （1）去分母，得$5(5x - 4) - 3(6x + 21) = 15$
去括号，得$25x - 20 - 18x - 63 = 15$
移项，得$25x - 18x = 15 + 20 + 63$
合并同类项，得$7x = 98$
系数化为1，得$x = 14$
（2）去括号，得$x - \frac{1}{2}(x - \frac{1}{2}x + \frac{1}{4}) = 2$
$x - \frac{1}{2}(\frac{1}{2}x + \frac{1}{4}) = 2$
$x - \frac{1}{4}x - \frac{1}{8} = 2$
移项，得$x - \frac{1}{4}x = 2 + \frac{1}{8}$
合并同类项，得$\frac{3}{4}x = \frac{17}{8}$
系数化为1，得$x = \frac{17}{6}$