20. (6分)张阿姨为了方便乘坐公交车,办了一张公交卡,以充电子钱包的方式存入50元.若她乘车的次数用$n$表示,则她每次乘车后卡内的余额$y$(单位:元)如下表所示.
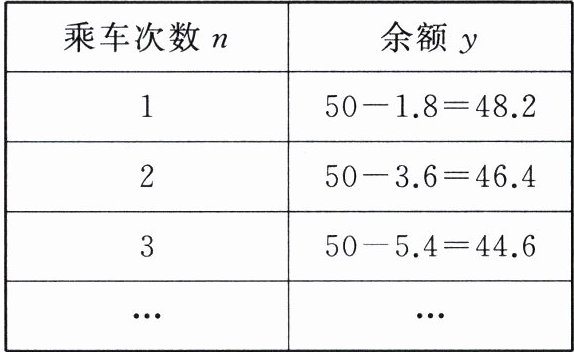
(1)张阿姨每次用公交卡乘车需要元.
(2)用式子表示张阿姨用公交卡的乘车次数$n$与余额$y$的关系.
(3)张阿姨乘车18次后,卡内还剩多少钱?张阿姨最多还能再乘几次公交车?

(1)张阿姨每次用公交卡乘车需要元.
(2)用式子表示张阿姨用公交卡的乘车次数$n$与余额$y$的关系.
(3)张阿姨乘车18次后,卡内还剩多少钱?张阿姨最多还能再乘几次公交车?
答案:
(1) 1.8
(2) $y = 50 - 1.8n$
(3) 17.6 元,9 次
(1) 1.8
(2) $y = 50 - 1.8n$
(3) 17.6 元,9 次
21. (8分)解答下列问题.
(1)已知$a = 3$,$b = -\frac{1}{2}$,求代数式$a^2 + 2ab + b^2$的值.
(2)已知$(2a - 1)^2 + |b + 3| = 0$,求代数式$\frac{ab}{a^2 - b^2}$的值.
(1)已知$a = 3$,$b = -\frac{1}{2}$,求代数式$a^2 + 2ab + b^2$的值.
(2)已知$(2a - 1)^2 + |b + 3| = 0$,求代数式$\frac{ab}{a^2 - b^2}$的值.
答案:
(1)当$a = 3$,$b = -\frac{1}{2}$时,
$\begin{aligned}a^2 + 2ab + b^2&=(a + b)^2\\&=(3 + (-\frac{1}{2}))^2\\&=(\frac{5}{2})^2\\&=\frac{25}{4}\end{aligned}$
(2)因为$(2a - 1)^2 + |b + 3| = 0$,且$(2a - 1)^2 \geq 0$,$|b + 3| \geq 0$,
所以$2a - 1 = 0$,$b + 3 = 0$,
解得$a = \frac{1}{2}$,$b = -3$。
$\begin{aligned}\frac{ab}{a^2 - b^2}&=\frac{ab}{(a + b)(a - b)}\\&=\frac{\frac{1}{2}×(-3)}{(\frac{1}{2} + (-3))(\frac{1}{2} - (-3))}\\&=\frac{-\frac{3}{2}}{(-\frac{5}{2})×\frac{7}{2}}\\&=\frac{-\frac{3}{2}}{-\frac{35}{4}}\\&=\frac{3}{2}×\frac{4}{35}\\&=\frac{6}{35}\end{aligned}$
$\begin{aligned}a^2 + 2ab + b^2&=(a + b)^2\\&=(3 + (-\frac{1}{2}))^2\\&=(\frac{5}{2})^2\\&=\frac{25}{4}\end{aligned}$
(2)因为$(2a - 1)^2 + |b + 3| = 0$,且$(2a - 1)^2 \geq 0$,$|b + 3| \geq 0$,
所以$2a - 1 = 0$,$b + 3 = 0$,
解得$a = \frac{1}{2}$,$b = -3$。
$\begin{aligned}\frac{ab}{a^2 - b^2}&=\frac{ab}{(a + b)(a - b)}\\&=\frac{\frac{1}{2}×(-3)}{(\frac{1}{2} + (-3))(\frac{1}{2} - (-3))}\\&=\frac{-\frac{3}{2}}{(-\frac{5}{2})×\frac{7}{2}}\\&=\frac{-\frac{3}{2}}{-\frac{35}{4}}\\&=\frac{3}{2}×\frac{4}{35}\\&=\frac{6}{35}\end{aligned}$
查看更多完整答案,请扫码查看


