《2025年53天天练四年级数学上册苏教版》

5 你认为她说得对吗？请说明你的理由,可以写一写或画一画。

答案： 5.答:我认为她说得不对。因为平角和周角都是角的一种，角是由一点引出的两条射线组成的图形。(理由合理即可)

6 学校举行放风筝比赛,同学们所用的风筝线的长度都是 30 米,假设他们都把风筝线放到最长。下图是甲同学比赛时的情景。
(1)量一量,甲同学的风筝线与地面的较小夹角是( )°。
(2)画一画,乙同学的风筝线与地面的较小夹角是$50^{\circ }$,请你在图中画出来。
(3)想一想,如果丙同学的风筝线与地面的较小夹角是$25^{\circ }$,那么他的风筝飞得比乙同学的( )。我发现风筝线与地面的较小夹角越大,风筝飞得越( )。

答案：
6.
(1)70
(2)示例:
(3)低　高

7 上面是一张长方形纸折起来后的图形,已知$∠2= 110^{\circ }$,那么$∠1$是多少度?

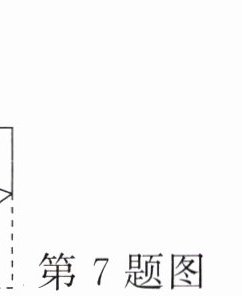
答案： 7.(180°−110°)÷2=35°
答:∠1是35°。

8 如右图,$∠1+∠2= 140^{\circ },∠2+∠3= 120^{\circ },$
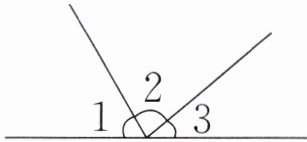
$∠2= $(80)°。

答案： 8.80
解析　由题目可知,(∠1+∠2)+(∠2+∠3)=140°+120°=260°,∠1+∠2+∠3=180°,∠2=(∠1+∠2)+(∠2+∠3)−(∠1+∠2+∠3)=260°−180°=80°。也可以先求出∠3的度数，再求出∠1的度数，最后用180°减去∠3和∠1的度数。

9 用一把长 15 厘米的尺子可以画出比它长的线段,那么用一个常规量角器可以画出一个$250^{\circ }$的角吗？请你以点 A 为顶点,想办法画一画。(保留作图痕迹)

答案：
9.示例:
解析　可以先画出一个平角,再用量角器画出70°的角(如上图);也可以用量角器画出110°的角，周角减去这个角就是250°的角;还可以用量角器先画出100°的角，再画出150°的角。除上面的画法，还有许多其他画法。