《2025年拔尖特训八年级物理上册苏科版》

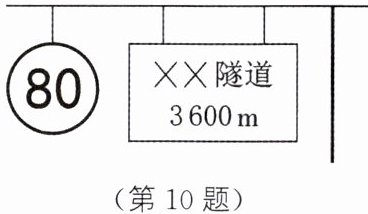
10. 如图所示为小丽开车即将到达隧道口时所发现的交通标志牌。
(1)请你解释两个标志牌上数字的含义。
(2)若以恒定速度通过该隧道所用的时间为3min,请你用两种不同的方法,通过计算判断小丽开车是否超速。(忽略车身长度)

答案： 解析:
(1)“80”表示汽车通过隧道时,最大速度不能超过$80\ km/h$;“3600”表示该隧道全长为$3600\ m$。
(2)方法一:汽车的速度$v=\frac{s}{t}=$$\frac{3600\ m}{3× 60\ s}=20\ m/s=72\ km/h＜80\ km/h$,因此没有超速;方法二:以$80\ km/h$的速度行驶$3\ min$,行驶的路程$s'=$$v't=80\ km/h× \frac{1}{20}\ h=4000\ m＞$$3600\ m$,故小丽开车的速度小于$80\ km/h$,没有超速。

11. 火车以20m/s的速度沿某一段直线轨道驶向道口,为了提醒看守道口的工作人员,司机在距道口940m处开始拉响汽笛,每次汽笛声持续1s,停5s,再次拉响汽笛。当道口工作人员听到第三次汽笛声结束时,火车与道口间的距离为______m。道口工作人员听到第一次和第二次汽笛声的时间间隔为______s。(已知声波在空气中传播的速度为340m/s)

答案： 640 5.65 解析：火车第三次鸣笛结束时,火车前进的时间$t_{总}=1\ s+$$5\ s+1\ s+5\ s+1\ s=13\ s$,则火车通过的路程$s_{1}=vt_{总}=20\ m/s× 13\ s=$$260\ m$,第三次鸣笛结束时火车距离工作人员$s=940\ m-260\ m=680\ m$。声音传到工作人员处所需时间$t=$$\frac{s}{v_{声}}=\frac{680\ m}{340\ m/s}=2\ s$,所以火车又前进了$2\ s$,此时通过的路程$s_{2}=vt=$$20\ m/s× 2\ s=40\ m$,火车此时距离道口$s'=680\ m-40\ m=640\ m$。从第一次鸣笛开始计时,第一次听到是在第一次鸣笛后$t_{1}=\frac{s_{总}}{v_{声}}=\frac{940\ m}{340\ m/s}\approx$$2.76\ s$,第二次鸣笛时火车与工作人员的距离$s_{3}=940\ m-20\ m/s×$$(1\ s+5\ s)=820\ m$,第二次鸣笛时已用时$t_{2}=1\ s+5\ s=6\ s$,第二次听到是在第二次鸣笛后$t_{3}=\frac{s_{3}}{v_{声}}=\frac{820\ m}{340\ m/s}\approx$$2.41\ s$,从第一次鸣笛到第二次听到鸣笛用时$t_{4}=6\ s+2.41\ s=8.41\ s$,听到这两次汽笛声的时间间隔,还要在$8.41\ s$中减掉第一次汽笛声传播用的时间,故$\Delta t=t_{4}-t_{1}=8.41\ s-$$2.76\ s=5.65\ s$。

12. 某款功能强大的物理实验手机软件能够自动记录下所接收到的两次响声之间的时间间隔：当手机接收到第一次响声时便自动计时,当再次接收到响声时计时自动停止(类似于使用秒表时的启动和停止),由于对声音的响应非常灵敏,计时可精确到0.001s。甲、乙两人使用手机在空旷安静的广场上测量声音的传播速度。他们分别站在间距测量值为s的A、B两处,打开手机软件做好计时准备。甲先在手机边击掌一次,乙听到击掌声之后,也在手机边击掌一次。甲、乙两手机均有效记录下了两次掌声的时间间隔,分别为t甲、t乙。

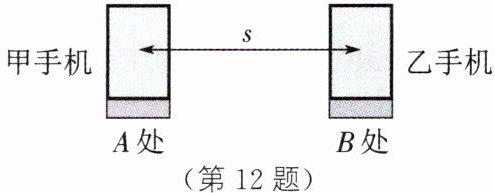
(1)若空气中的声速为340m/s,则0.001s内声音的传播距离为______m。
(2)本实验中两手机所记录的时间大小关系是t甲______(＞/= /＜)t乙。
(3)测得空气中声音的传播速度v声= ______。(用s、t甲、t乙表示)

答案：
(1)0.34
(2)$＞$
(3)$\frac{2s}{t_{甲}-t_{乙}}$
解析:
(1)根据$s=vt$可知,$0.001\ s$内声音的传播距离$s=vt=340\ m/s×$$0.001\ s=0.34\ m$。
(2)依题意可知,甲手机记录的时间$t_{甲}$是声音在空气中传播一个来回所用的时间与乙手机记录的时间$t_{乙}$之和,故$t_{甲}＞t_{乙}$。
(3)设声音在空气中的传播速度为$v_{声}$,则$v_{声}t_{甲}-v_{声}t_{乙}=2s$,解得$v_{声}=\frac{2s}{t_{甲}-t_{乙}}$。