11. 在等腰三角形ABC中,AB= AC,若∠A= 40°,则∠B= ______。
答案:
70°
12. 如图,在△ABC中,AB= AC,AD是中线,若∠C= 72°,则∠BAD的度数为______。
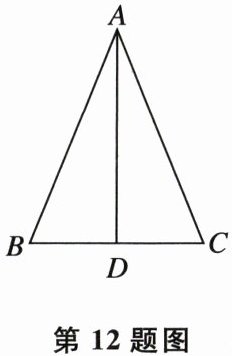

答案:
18°
13. 写出命题“如果$a^2= b^2,$那么a= b”的逆命题:______。
答案:
如果a=b,那么a²=b²
14. 如图,在3×3的正方形网格中,点A,B在格点上,若点C也在格点上,且△ABC是等腰三角形,则符合条件的点C的个数为______。


答案:
3
15. 如图,在△ABC中,∠C= 90°,D是BC上的点,若BD= 6,DC= 9,则$AB^2-AD^2$的值为______。


答案:
144
16. 小丽从一张等腰三角形纸片ABC(AB= AC)中恰好剪出五个小等腰三角形,如图所示,其中BC= BD,EC= EF= FG= DG= DA,则∠B= ______°。
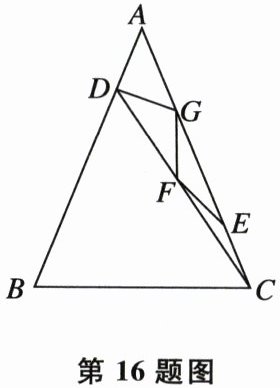

答案:
67.5【解析】设∠ECF=x,因为EC=EF,所以∠EFC=∠ECF=x,所以∠GEF=2x。因为EF=GF,所以∠FGE=∠GEF=2x,所以∠DFG=∠FGE+∠ECF=3x。因为DG=GF,所以∠GDF=∠DFG=3x,所以∠AGD=∠GDF+∠ECF=4x。因为DG=DA,所以∠A=4x,所以∠BDC=∠A+∠ECF=5x。因为BC=BD,所以∠BDC=∠BCD=5x,所以∠ACB=∠BCD+∠ECF=6x。因为AB=AC,所以∠B=∠ACB=6x,因为∠A+∠B+∠ACB=180°,所以4x+6x+6x=180°,解得x=$\frac{45}{4}$,所以∠B=67.5°。
17. (8分)如图,在△ABC中,AC= BC,点D在CB的延长线上,点E在AB上,∠D= ∠BED= 40°。求∠A的度数。


答案:
解:因为AC=BC,所以∠A=∠ABC。因为∠D=∠BED=40°,所以∠ABC=∠D+∠DEB=40°+40°=80°,所以∠A=80°。
18. (8分)在图1中补充2个小方块,在图2,3,4中均补充3个小方块,分别使它们成为轴对称图形。


答案:
解:补充的图形如下(答案不唯一)。


解:补充的图形如下(答案不唯一)。



19. (8分)如图,在△ABC中,AB= AC,BD是AC边上的高线。
(1)若∠C= 2∠A,求∠DBC的度数。
(2)设∠A= α,求∠DBC的度数。(用含α的代数式表示)

(1)若∠C= 2∠A,求∠DBC的度数。
(2)设∠A= α,求∠DBC的度数。(用含α的代数式表示)

答案:
(1)解:设∠A=α,则∠C=2α。因为AB=AC,所以∠ABC=∠C=2α。又因为在△ABC中,∠A+∠ABC+∠C=180°,所以5α=180°,所以α=36°,所以∠C=72°。因为BD⊥AC,所以∠DBC=90°-∠C=18°。
(2)解:因为AB=AC,∠A=α,所以∠ABC=$\frac{180°-α}{2}$=90°-$\frac{1}{2}$α。因为BD⊥AC,所以∠ABD=90°-α,所以∠DBC=∠ABC-∠ABD=90°-$\frac{1}{2}$α-(90°-α)=$\frac{1}{2}$α。
(1)解:设∠A=α,则∠C=2α。因为AB=AC,所以∠ABC=∠C=2α。又因为在△ABC中,∠A+∠ABC+∠C=180°,所以5α=180°,所以α=36°,所以∠C=72°。因为BD⊥AC,所以∠DBC=90°-∠C=18°。
(2)解:因为AB=AC,∠A=α,所以∠ABC=$\frac{180°-α}{2}$=90°-$\frac{1}{2}$α。因为BD⊥AC,所以∠ABD=90°-α,所以∠DBC=∠ABC-∠ABD=90°-$\frac{1}{2}$α-(90°-α)=$\frac{1}{2}$α。
查看更多完整答案,请扫码查看


