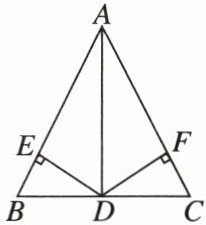
18.(8分)如图,在△ABC中,AB= AC,点D在BC上,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE= DF。求证:D是BC的中点。

答案:
证明:因为DE⊥AB,DF⊥AC,且DE = DF,
所以AD是∠BAC的平分线。
因为在△ABC中,AB = AC,
所以D是BC的中点。
所以AD是∠BAC的平分线。
因为在△ABC中,AB = AC,
所以D是BC的中点。
19.(8分)在正方形网格中,每个小正方形的顶点称为格点,顶点都在格点上的三角形叫作格点三角形,现有A,B两个格点,请以AB为边分别画出符合下列要求的格点三角形。
(1)在图1中画一个面积为4的直角三角形。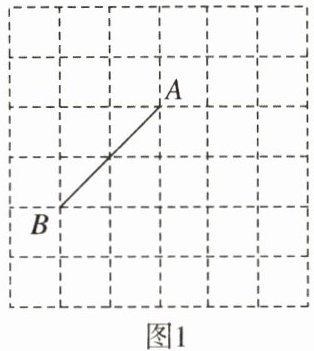
(2)在图2中画一个等腰(非直角)三角形,则这个等腰三角形的腰长为______。

(1)在图1中画一个面积为4的直角三角形。

(2)在图2中画一个等腰(非直角)三角形,则这个等腰三角形的腰长为______。

答案:
解:
(1)如图1,△ABC即为所求。
(2)如图2,△ABC即为所求,$CA = CB = \sqrt{1^{2} + 3^{2}} = \sqrt{10}$。
(答案不唯一)


解:
(1)如图1,△ABC即为所求。
(2)如图2,△ABC即为所求,$CA = CB = \sqrt{1^{2} + 3^{2}} = \sqrt{10}$。
(答案不唯一)


20.(8分)如图,已知线段a,利用直尺和圆规按照下列要求作出图形。(保留作图痕迹,不要求写作法)
(1)作一个等边三角形,边长为a。
(2)在第(1)题的图中,作一个∠α,使∠α= 30°。
(1)作一个等边三角形,边长为a。

(2)在第(1)题的图中,作一个∠α,使∠α= 30°。
答案:
解:
(1)如图,△ABC为所作。
(2)如图,∠α为所作。

解:
(1)如图,△ABC为所作。
(2)如图,∠α为所作。

21.(8分)在购物节来临之际,某商场计划采购甲、乙两种厨房小家电,已知购进6件甲种家电的费用与购进5件乙种家电的费用相同,购进1件甲种家电比购进1件乙种家电便宜100元。
(1)求这两种家电每件的进价分别是多少元。
(2)若该商场欲购进两种家电共100件,总金额不超过54000元,则该商场至少购进甲种家电多少件?
(1)求这两种家电每件的进价分别是多少元。
(2)若该商场欲购进两种家电共100件,总金额不超过54000元,则该商场至少购进甲种家电多少件?
答案:
解:
(1)设甲种家电每件的进价是x元,乙种家电每件的进价是y元,
由题意得$\begin{cases} 6x = 5y, \\ y - x = 100, \end{cases}$
解得$\begin{cases} x = 500, \\ y = 600. \end{cases}$
答:甲种家电每件的进价是500元,乙种家电每件的进价是600元。
(2)设该商场购进甲种家电m件,则购进乙种家电(100 - m)件,
由题意得,500m + 600(100 - m) ≤ 54000,
解得m ≥ 60。
答:该商场至少购进甲种家电60件。
(1)设甲种家电每件的进价是x元,乙种家电每件的进价是y元,
由题意得$\begin{cases} 6x = 5y, \\ y - x = 100, \end{cases}$
解得$\begin{cases} x = 500, \\ y = 600. \end{cases}$
答:甲种家电每件的进价是500元,乙种家电每件的进价是600元。
(2)设该商场购进甲种家电m件,则购进乙种家电(100 - m)件,
由题意得,500m + 600(100 - m) ≤ 54000,
解得m ≥ 60。
答:该商场至少购进甲种家电60件。
查看更多完整答案,请扫码查看


