22.(10分)图1是一个平分角的仪器,其中OD= OE,FD= FE。
(1)如图2,将仪器放置在△ABC上,使点O与顶点A重合,D,E分别在边AB,AC上,沿AF画一条射线AP,交BC于点P。AP是∠BAC的平分线吗?请判断并说明理由。
(2)如图3,在(1)的条件下,过点P作PQ⊥AB于点Q,若PQ= 6,AC= 9,△ABC的面积是60,求AB的长。

(1)如图2,将仪器放置在△ABC上,使点O与顶点A重合,D,E分别在边AB,AC上,沿AF画一条射线AP,交BC于点P。AP是∠BAC的平分线吗?请判断并说明理由。
(2)如图3,在(1)的条件下,过点P作PQ⊥AB于点Q,若PQ= 6,AC= 9,△ABC的面积是60,求AB的长。

答案:
解:
(1)AP是∠BAC的平分线,理由如下:
在△ADF和△AEF中,
$\begin{cases} AD = AE, \\ FD = FE, \\ AF = AF, \end{cases}$
所以△ADF≌△AEF(SSS)。
所以∠DAF = ∠EAF,
所以AP平分∠BAC。
(2)如图,过点P作PG⊥AC于点G。
因为AP平分∠BAC,PQ⊥AB,
所以PG = PQ = 6。
因为$S_{\triangle ABC} = S_{\triangle ABP} + S_{\triangle APC} = \frac{1}{2}AB\cdot PQ + \frac{1}{2}AC\cdot PG$,
所以$\frac{1}{2}AB×6 + \frac{1}{2}×9×6 = 60$,
所以AB = 11。

解:
(1)AP是∠BAC的平分线,理由如下:
在△ADF和△AEF中,
$\begin{cases} AD = AE, \\ FD = FE, \\ AF = AF, \end{cases}$
所以△ADF≌△AEF(SSS)。
所以∠DAF = ∠EAF,
所以AP平分∠BAC。
(2)如图,过点P作PG⊥AC于点G。
因为AP平分∠BAC,PQ⊥AB,
所以PG = PQ = 6。
因为$S_{\triangle ABC} = S_{\triangle ABP} + S_{\triangle APC} = \frac{1}{2}AB\cdot PQ + \frac{1}{2}AC\cdot PG$,
所以$\frac{1}{2}AB×6 + \frac{1}{2}×9×6 = 60$,
所以AB = 11。

23.(10分)【阅读理解】
已知a,b,c是三个实数,M{a,b,c}表示a,b,c这三个数的平均数,min{a,b,c}表示a,b,c这三个数中最小的数。
如,$M{-1,2,3}= \frac{-1+2+3}{3}= \frac{4}{3},$min{-1,2,3}= -1;$M{-1,2,a}= \frac{-1+2+a}{3}= \frac{a+1}{3},$$min{-1,2,a}= \begin{cases} a(a\leq-1) \\ -1(a>-1) \end{cases} 。$
解决下列问题:
(1)若min{2,2x+2,4-2x}= 2,求x的取值范围。
(2)若M{2,x+1,2x}= min{2,x+1,2x},求x的值。
(3)由(2)可得结论:“若M{a,b,c}= min{a,b,c},则______”(填a,b,c的大小关系)。运用这个结论解决问题:若M{2x+y+2,x+2y,2x-y}= min{2x+y+2,x+2y,2x-y},求x+y的值。
已知a,b,c是三个实数,M{a,b,c}表示a,b,c这三个数的平均数,min{a,b,c}表示a,b,c这三个数中最小的数。
如,$M{-1,2,3}= \frac{-1+2+3}{3}= \frac{4}{3},$min{-1,2,3}= -1;$M{-1,2,a}= \frac{-1+2+a}{3}= \frac{a+1}{3},$$min{-1,2,a}= \begin{cases} a(a\leq-1) \\ -1(a>-1) \end{cases} 。$
解决下列问题:
(1)若min{2,2x+2,4-2x}= 2,求x的取值范围。
(2)若M{2,x+1,2x}= min{2,x+1,2x},求x的值。
(3)由(2)可得结论:“若M{a,b,c}= min{a,b,c},则______”(填a,b,c的大小关系)。运用这个结论解决问题:若M{2x+y+2,x+2y,2x-y}= min{2x+y+2,x+2y,2x-y},求x+y的值。
答案:
解:
(1)根据题意,得$\begin{cases} 2x + 2 \geq 2, \\ 4 - 2x \geq 2, \end{cases}$
解得0 ≤ x ≤ 1。
(2)M{2, x + 1, 2x} = $\frac{2 + x + 1 + 2x}{3} = x + 1$,M{2, x + 1, 2x} = min{2, x + 1, 2x},
所以min{2, x + 1, 2x} = x + 1,
所以$\begin{cases} x + 1 \leq 2, \\ x + 1 \leq 2x, \end{cases}$
解得x = 1。
(3)根据
(2)可得a = b = c。
故答案为a = b = c。
根据题意,得$\begin{cases} 2x + y + 2 = x + 2y, \\ x + 2y = 2x - y, \end{cases}$
解得$\begin{cases} x = -3, \\ y = -1, \end{cases}$
所以x + y = -3 + (-1) = -4。
(1)根据题意,得$\begin{cases} 2x + 2 \geq 2, \\ 4 - 2x \geq 2, \end{cases}$
解得0 ≤ x ≤ 1。
(2)M{2, x + 1, 2x} = $\frac{2 + x + 1 + 2x}{3} = x + 1$,M{2, x + 1, 2x} = min{2, x + 1, 2x},
所以min{2, x + 1, 2x} = x + 1,
所以$\begin{cases} x + 1 \leq 2, \\ x + 1 \leq 2x, \end{cases}$
解得x = 1。
(3)根据
(2)可得a = b = c。
故答案为a = b = c。
根据题意,得$\begin{cases} 2x + y + 2 = x + 2y, \\ x + 2y = 2x - y, \end{cases}$
解得$\begin{cases} x = -3, \\ y = -1, \end{cases}$
所以x + y = -3 + (-1) = -4。
24.(12分)在△ABC中,∠BAC= 90°,AB= AC,BC= 6,在直线BC上有一点D,连结AD,以A为直角顶点向AD右侧作等腰直角三角形ADE,连结ED,EC。
(1)如图1,当点D在线段BC上时,求证:△ABD≌△ACE。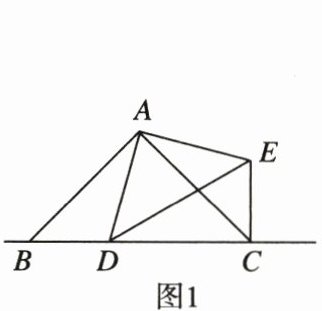
(2)如图2,点D在线段BC的延长线上,当EC平分∠AED时,求CD的长。
(3)如图3,点D在线段CB的延长线上,AE与BC相交于点F,且CF= 1,在直线CE上有一点G,求AG+FG的最小值。

(1)如图1,当点D在线段BC上时,求证:△ABD≌△ACE。

(2)如图2,点D在线段BC的延长线上,当EC平分∠AED时,求CD的长。

(3)如图3,点D在线段CB的延长线上,AE与BC相交于点F,且CF= 1,在直线CE上有一点G,求AG+FG的最小值。

答案:
解:
(1)证明:因为∠BAC = 90°,∠DAE = 90°,
所以∠BAC = ∠DAE,
所以∠BAD + ∠CAD = ∠CAE + ∠CAD,
即∠BAD = ∠CAE。
在△ABD和△ACE中,
$\begin{cases} AB = AC, \\ \angle BAD = \angle CAE, \\ AD = AE, \end{cases}$
所以△ABD≌△ACE(SAS)。
(2)因为∠BAC = 90°,AB = AC,∠DAE = 90°,AD = AE,
所以∠ACB = 45°,∠AED = 45°。
因为EC平分∠AED,
所以$\angle AEC = \frac{1}{2}\angle AED = 22.5^{\circ}$。
由
(1)同理可知,△ABD≌△ACE,
所以∠ADC = ∠AEC = 22.5°,
所以∠CAD = ∠ACB - ∠ADC = 22.5°,
所以∠ADC = ∠CAD,所以$CD = AC = \frac{BC}{\sqrt{2}} = \frac{6}{\sqrt{2}}$。
(3)作F关于直线CE的对称点F',连结AF'(图略),AF'即为AG + FG的最小值。
作AM⊥BC,易得AM = 3,MF' = 4,
由勾股定理可得$(AG + FG)_{min} = AF' = 5$。
(1)证明:因为∠BAC = 90°,∠DAE = 90°,
所以∠BAC = ∠DAE,
所以∠BAD + ∠CAD = ∠CAE + ∠CAD,
即∠BAD = ∠CAE。
在△ABD和△ACE中,
$\begin{cases} AB = AC, \\ \angle BAD = \angle CAE, \\ AD = AE, \end{cases}$
所以△ABD≌△ACE(SAS)。
(2)因为∠BAC = 90°,AB = AC,∠DAE = 90°,AD = AE,
所以∠ACB = 45°,∠AED = 45°。
因为EC平分∠AED,
所以$\angle AEC = \frac{1}{2}\angle AED = 22.5^{\circ}$。
由
(1)同理可知,△ABD≌△ACE,
所以∠ADC = ∠AEC = 22.5°,
所以∠CAD = ∠ACB - ∠ADC = 22.5°,
所以∠ADC = ∠CAD,所以$CD = AC = \frac{BC}{\sqrt{2}} = \frac{6}{\sqrt{2}}$。
(3)作F关于直线CE的对称点F',连结AF'(图略),AF'即为AG + FG的最小值。
作AM⊥BC,易得AM = 3,MF' = 4,
由勾股定理可得$(AG + FG)_{min} = AF' = 5$。
查看更多完整答案,请扫码查看


