《2025年精彩三年就练这一本八年级数学上册浙教版》

1. 体育是一个锻炼身体,增强体质,培养道德和意志品质的教育过程,是培养全面发展的人的一个重要方面,下列体育图标是轴对称图形的是( )

答案： C

2. 已知一次函数$y= -2x-2$,当自变量$x= -2$时,函数值是( )

A.$-2$
B.$2$
C.$-6$
D.$6$

答案： B

3. 对于命题“如果$a＜1$,那么$a^2＜1$”,能说明它是假命题的反例是( )

A.$a= -2$
B.$a= 2$
C.$a= -\frac{1}{2}$
D.$a= 0$

答案： A

4. 已知$x＞y$,则下列不等式成立的是( )

A.$-2x＞-2y$
B.$x-3＞y-2$
C.$5-x＞5-y$
D.$3x-3＞3y-3$

答案： D

5. 如图,若函数$y= kx+b的图象经过点A(-3,2)$,则关于$x的不等式kx+b＜2$的解集为( )


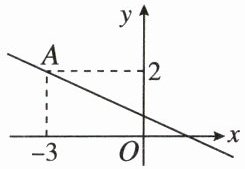
A.$x＞-3$
B.$x＜-3$
C.$x＞2$
D.$x＜2$

答案： A

6. 不等式组$\begin{cases}2x\geq-2\\x+3＜4\end{cases} $的解集在数轴上表示为( )

答案： B

7. 一次函数$y= kx+b与正比例函数y= kbx$在同一坐标系中的图象可能为( )

答案： A

8. 有甲、乙、丙三人,它们所在的位置不同,他们三人都以相同的单位建立不同的坐标系,甲说:“如果以我为坐标原点,乙的位置是$(4,3)$”;丙说:“以我为坐标原点,乙的位置是$(-3,-4)$”;如果以乙为坐标原点,那么甲和丙的位置分别是( )

A.$(3,4),(-3,-4)$
B.$(4,-3),(3,-4)$
C.$(-3,-4),(4,3)$
D.$(-4,-3),(3,4)$

答案： D

9. 若点$A(a,y_1),B(2a,y_2)都在一次函数y= -2ax+a(a\neq0)$的图象上,则$y_1,y_2$的大小关系( )

A.是$y_1＞y_2$
B.是$y_1= y_2$
C.是$y_1＜y_2$
D.不确定

答案： A

10. 如图,四个全等的直角三角形与中间的小正方形$EFGH拼成了一个大正方形ABCD$,连结$AC$,交$BE于点P$,若正方形$ABCD的面积为30$,$AE+BE= 7$。则$S_{\triangle CFP}-S_{\triangle AEP}$的值是( )


A.$5.5$
B.$6.5$
C.$7$
D.$7.5$

答案： A 【解析】因为正方形 ABCD 的面积为 30，所以 $AB^{2}=30$。设 $AE=x$，因为 $AE+BE=7$，所以 $BE=7-x$。在 $Rt\triangle AEB$ 中，由勾股定理得 $AE^{2}+BE^{2}=AB^{2}$，所以 $x^{2}+(7-x)^{2}=30$，所以 $2x^{2}-14x=-19$。因为 $AH\perp BE$，$BE\perp CF$，所以 $AH// CF$，所以 $\angle EAP=\angle GCM$，因为四个全等的直角三角形与中间的小正方形 EFGH 拼成一个大正方形 ABCD，所以 $\triangle AEB\cong \triangle CGD$，所以 $AE=CG$，所以 $\triangle AEP\cong \triangle CGM$，所以 $S_{\triangle AEP}=S_{\triangle CGM}$，$EP=MG$，所以 $S_{\triangle CFP}-S_{\triangle AEP}=S_{\triangle CFP}-S_{\triangle CGM}=S_{梯形 FPMG}=\frac{1}{2}(MG+PF)\cdot FG=\frac{1}{2}EF\cdot FG=\frac{1}{2}S_{正方形 EHGF}$。因为 $S_{正方形 EHGF}=S_{正方形 ABCD}-4S_{\triangle AEB}=30-4×\frac{1}{2}x\cdot (7-x)=30-2x(7-x)=30-19=11$，则 $S_{\triangle CFP}-S_{\triangle AEP}$ 的值是 5.5。