第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
5. 小科设计实验来探究气泡的运动规律。如图所示,他在细玻璃管中注入水,管中留一个小气泡,将玻璃管翻转后,观察气泡的运动情况。

气泡的运动快慢到底与哪些因素有关呢?他作出了如下猜想:
猜想一:跟气泡的大小有关。
猜想二:跟玻璃管与水平面的倾角有关。
为了便于研究,他在玻璃管上做上记号A、B,测出气泡经过AB段的时间。实验数据记录如下表所示。已知气泡的直径约为2cm。
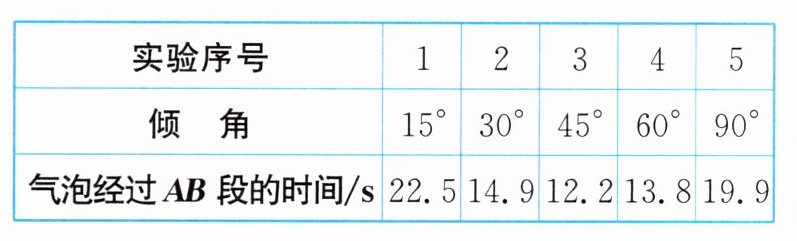
(1) 实验中,除刻度尺、量角器外,还需要的测量器材为
(2) 分析表中的数据,可以发现气泡运动的快慢随倾角的变化关系:
(3) 若用上述器材探究气泡的运动快慢与气泡大小的关系,则需要控制

气泡的运动快慢到底与哪些因素有关呢?他作出了如下猜想:
猜想一:跟气泡的大小有关。
猜想二:跟玻璃管与水平面的倾角有关。
为了便于研究,他在玻璃管上做上记号A、B,测出气泡经过AB段的时间。实验数据记录如下表所示。已知气泡的直径约为2cm。

(1) 实验中,除刻度尺、量角器外,还需要的测量器材为
秒表
,AB段的路程为80.0
cm。(2) 分析表中的数据,可以发现气泡运动的快慢随倾角的变化关系:
气泡大小相同时,随着倾角变大,运动速度先变大后变小
。(3) 若用上述器材探究气泡的运动快慢与气泡大小的关系,则需要控制
玻璃管与水平面的倾角
相同。
答案:
(1) 秒表 80.0
(2) 气泡大小相同时,随着倾角变大,运动速度先变大后变小
(3) 玻璃管与水平面的倾角
(1) 秒表 80.0
(2) 气泡大小相同时,随着倾角变大,运动速度先变大后变小
(3) 玻璃管与水平面的倾角
6. 小明爸爸开车载着他从郊外到市区,汽车进入某国道,如图所示为该国道某直线路段的一处测速仪,测速仪内有能发射和接收超声波的传感器。汽车以某一速度v远离测速仪,在距测速仪62m时,测速仪发出超声波信号,经汽车反射后接收到超声波信号,其间用时0.4s。已知此路段限速为80km/h,超声波的速度为340m/s。试计算并说明汽车在此路段是否超速。
根据 $v = \frac{s}{t}$ 得,超声波在 $t = \frac{1}{2}×0.4 s =$
根据 $v = \frac{s}{t}$ 得,超声波在 $t = \frac{1}{2}×0.4 s =$
0.2 s
内通过的距离 $s = vt = 340 m/s×$0.2 s
=68 m
,汽车在 0.2 s 内通过的距离 $s_{汽车} = s - s_{0} =$68 m
-62 m
=6 m
,汽车行驶的速度 $v_{汽车} = \frac{s_{汽车}}{t} = \frac{6 m}{0.2 s} =$30 m/s
=108 km/h
> 80 km/h,所以该汽车在此路段超速
答案:
根据 $v = \frac{s}{t}$ 得,超声波在 $t = \frac{1}{2}×0.4 s = 0.2 s$ 内通过的距离 $s = vt = 340 m/s×0.2 s = 68 m$,汽车在 0.2 s 内通过的距离 $s_{汽车} = s - s_{0} = 68 m - 62 m = 6 m$,汽车行驶的速度 $v_{汽车} = \frac{s_{汽车}}{t} = \frac{6 m}{0.2 s} = 30 m/s = 108 km/h > 80 km/h$,所以该汽车在此路段超速
7. 地震时,震源处同时产生并向各个方向发出纵波和横波,纵波的传播速度取$7×10^3m/s,$横波的传播速度取$3.5×10^3m/s。$如图所示,某市地震局于当日21:46:07探测到纵波,于当日21:46:09探测到横波。求:
(1) 地震局与震源之间的距离为
(2) 震源发生地震的时刻为当日

(1) 地震局与震源之间的距离为
14000m
。(2) 震源发生地震的时刻为当日
21:46:05
。
答案:
(1) 由题意可得,两列波到达的时间差 $\Delta t = 21:46:09 - 21:46:07 = 2 s$,设地震局到震源的距离为 $s$,由速度公式可得, $\frac{s}{v_{横}} - \frac{s}{v_{纵}} = 2 s$,即 $\frac{s}{3.5×10^{3} m/s} - \frac{s}{7×10^{3} m/s} = 2 s$,解得 $s = 14 000 m$
(2) 由速度公式知 $t_{纵} = \frac{s}{v_{纵}} = \frac{14 000 m}{7×10^{3} m/s} = 2 s$,21:46:07 - 2 s = 21:46:05,震源发生地震的时刻为当日 21:46:05
(1) 由题意可得,两列波到达的时间差 $\Delta t = 21:46:09 - 21:46:07 = 2 s$,设地震局到震源的距离为 $s$,由速度公式可得, $\frac{s}{v_{横}} - \frac{s}{v_{纵}} = 2 s$,即 $\frac{s}{3.5×10^{3} m/s} - \frac{s}{7×10^{3} m/s} = 2 s$,解得 $s = 14 000 m$
(2) 由速度公式知 $t_{纵} = \frac{s}{v_{纵}} = \frac{14 000 m}{7×10^{3} m/s} = 2 s$,21:46:07 - 2 s = 21:46:05,震源发生地震的时刻为当日 21:46:05
8. 研究发现,当车辆以相同速度行驶时,刹车后减速行驶的路程相同。经测定,某志愿者的刹车反应时间是0.4s(图中“反应过程”指志愿者从发现情况到开始减速的过程,对应的时间为反应时间)。
(1) 在某次试验中,该志愿者驾车以72km/h的速度在试验场的水平路面上匀速行驶,从发现情况到汽车停止,行驶距离为33m,则经过
(2) 若志愿者边打电话边驾车,以72km/h的速度在试验场的水平路面上匀速行驶,从发现情况到汽车停止,行驶距离为39m,则此次志愿者的反应时间是
(3) 由此研究可知,驾驶车辆时打电话,驾驶员的刹车反应会如何变化?
(1) 在某次试验中,该志愿者驾车以72km/h的速度在试验场的水平路面上匀速行驶,从发现情况到汽车停止,行驶距离为33m,则经过
8m
的距离后汽车才开始减速?(2) 若志愿者边打电话边驾车,以72km/h的速度在试验场的水平路面上匀速行驶,从发现情况到汽车停止,行驶距离为39m,则此次志愿者的反应时间是
0.7s
?(3) 由此研究可知,驾驶车辆时打电话,驾驶员的刹车反应会如何变化?
驾驶时打电话,驾驶员的刹车反应会变慢
答案:
(1) $v = 72 km/h = 20 m/s$, $s = vt = 20 m/s×0.4 s = 8 m$
(2) $s' = 39 m - 33 m + 8 m = 14 m$, $t' = \frac{s'}{v} = \frac{14 m}{20 m/s} = 0.7 s$
(3) 驾驶时打电话,驾驶员的刹车反应会变慢
(1) $v = 72 km/h = 20 m/s$, $s = vt = 20 m/s×0.4 s = 8 m$
(2) $s' = 39 m - 33 m + 8 m = 14 m$, $t' = \frac{s'}{v} = \frac{14 m}{20 m/s} = 0.7 s$
(3) 驾驶时打电话,驾驶员的刹车反应会变慢
查看更多完整答案,请扫码查看


