第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
6. (绍兴期中)小石用一把刻度均匀的米尺量得一张小方桌每边的长为0.680m,然后,他将这把米尺与标准尺进行比较,发现这把米尺的实际长度为0.995m。这张小方桌每边的实际长度为
0.677
m。
答案:
0.677 解析: 使用刻度尺读数时, 应估读至分度值的下一位, 根据这把米尺量得的“小方桌每边的长为 $ 0.680 \, \text{m} $”可知该米尺的分度值为 $ 1 \, \text{cm} $, 相当于米尺上共有 100 小格, 小方桌的边长占 68 小格。将米尺与标准尺进行比较后可知此米尺的实际长度为 $ 0.995 \, \text{m} $, 则该米尺上每一小格的真实值为 $ 0.995 \, \text{cm} $。小方桌每边的实际长度 $ L = 68 × 0.995 \, \text{cm} = 67.66 \, \text{cm} \approx 0.677 \, \text{m} $。
7. 跨学科实践 日常生活 小应在家中自制量筒。如图所示,他分别选择了玻璃杯和塑料瓶作为材料,通过测量发现,玻璃杯最多可以装200mL水,塑料瓶最多可以装450mL水。下列说法中,正确的是(
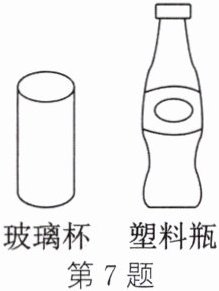
A.玻璃杯的量程大,刻度不均匀
B.玻璃杯的量程小,刻度均匀
C.塑料瓶的量程大,刻度均匀
D.塑料瓶的量程小,刻度不均匀
B
)
A.玻璃杯的量程大,刻度不均匀
B.玻璃杯的量程小,刻度均匀
C.塑料瓶的量程大,刻度均匀
D.塑料瓶的量程小,刻度不均匀
答案:
B 解析: 玻璃杯最多可以装 $ 200 \, \text{mL} $ 水, 塑料瓶最多可以装 $ 450 \, \text{mL} $ 水, 可见玻璃杯的量程小于塑料瓶的量程; 玻璃杯是上下粗细均匀的, 与量筒相似, 所以可知其刻度是均匀的, 塑料瓶上下粗细不均匀, 与量杯进行比较, 发现其刻度不均匀。
8. 实验室用排水法测量形状不规则的小石块的体积时,老师总是强调先要在量筒中加入“适量的水”。
(1)“适量”是指能用排水法测量出小石块体积的水量范围,其中最多水量是指小石块放入量筒后,液面上升到最大刻度线处时的水量;最少水量是指小石块放入量筒后,量筒内的液面上升到
(2)现有100mL的量筒,用排水法测量$15cm^3$的形状不规则的小石块的体积,需加入“适量的水”的体积可能为(
A. 5mL
B. 50mL
C. 80mL
D. 95mL
(1)“适量”是指能用排水法测量出小石块体积的水量范围,其中最多水量是指小石块放入量筒后,液面上升到最大刻度线处时的水量;最少水量是指小石块放入量筒后,量筒内的液面上升到
刚好浸没石块
时的水量。(2)现有100mL的量筒,用排水法测量$15cm^3$的形状不规则的小石块的体积,需加入“适量的水”的体积可能为(
ABC
)(填字母)。A. 5mL
B. 50mL
C. 80mL
D. 95mL
答案:
(1) 刚好浸没石块
(2) ABC 解析:
(1) 最少水量是指物体放入量筒后, 量筒内液面上升到刚好浸没物体时的水量。
(2) 利用 $ 100 \, \text{mL} $ 的量筒, 用排水法测量本题中 $ 15 \, \text{cm}^3 $ 的小石块的体积, 石块放入 $ 95 \, \text{mL} $ 的水中后两者的总体积会超过量筒的最大测量值 $ (V_{\text{总}} = 95 \, \text{mL} + 15 \, \text{cm}^3 = 95 \, \text{mL} + 15 \, \text{mL} = 110 \, \text{mL} > 100 \, \text{mL}) $, 所以 D 不合适; $ 5 \, \text{mL} $、$ 50 \, \text{mL} $、$ 80 \, \text{mL} $ 的水都可能浸没 $ 15 \, \text{cm}^3 $ 的小石块, 且小石块和水的总体积小于量筒的最大测量值 $ 100 \, \text{mL} $, 故“适量的水”可能为 $ 5 \, \text{mL} $、$ 50 \, \text{mL} $、$ 80 \, \text{mL} $。
(1) 刚好浸没石块
(2) ABC 解析:
(1) 最少水量是指物体放入量筒后, 量筒内液面上升到刚好浸没物体时的水量。
(2) 利用 $ 100 \, \text{mL} $ 的量筒, 用排水法测量本题中 $ 15 \, \text{cm}^3 $ 的小石块的体积, 石块放入 $ 95 \, \text{mL} $ 的水中后两者的总体积会超过量筒的最大测量值 $ (V_{\text{总}} = 95 \, \text{mL} + 15 \, \text{cm}^3 = 95 \, \text{mL} + 15 \, \text{mL} = 110 \, \text{mL} > 100 \, \text{mL}) $, 所以 D 不合适; $ 5 \, \text{mL} $、$ 50 \, \text{mL} $、$ 80 \, \text{mL} $ 的水都可能浸没 $ 15 \, \text{cm}^3 $ 的小石块, 且小石块和水的总体积小于量筒的最大测量值 $ 100 \, \text{mL} $, 故“适量的水”可能为 $ 5 \, \text{mL} $、$ 50 \, \text{mL} $、$ 80 \, \text{mL} $。
9. *小金感觉自己发热了,用体温计测量体温,结果为38.5℃,疑惑片刻后他甩了甩体温计,再次测量,结果为37.8℃,小金的体温是(
A.38.5℃
B.38.5℃以上
C.不超过37.8℃
D.在37.8~38.5℃的范围内
C
)A.38.5℃
B.38.5℃以上
C.不超过37.8℃
D.在37.8~38.5℃的范围内
答案:
C 解析: 根据体温计的特点, 使用前用力甩几下, 玻璃泡上方的水银才能回到玻璃泡中。直接用没有甩过的体温计来测量体温, 若体温高于体温计原来的示数, 则体温计中的水银柱会上升, 测量结果是比较准确的; 若体温不高于体温计的示数, 则体温计中的水银柱不会下降, 依然显示原来的示数, 所以小金的体温应该低于或等于 $ 37.8^{\circ} \text{C} $, 故 C 正确。
易错提示
体温计的使用
体温计使用前必须甩几下, 并且甩到 $ 35^{\circ} \text{C} $ 以下, 倘若不甩, 由于体温计玻璃泡的上方有个缩口, 使体温计离开人体时, 水银柱在缩口处断开, 水银柱只能上不能下, 故体温计只能准确测量比原来示数高的体温, 低于原来示数的体温是无法测量的。
易错提示
体温计的使用
体温计使用前必须甩几下, 并且甩到 $ 35^{\circ} \text{C} $ 以下, 倘若不甩, 由于体温计玻璃泡的上方有个缩口, 使体温计离开人体时, 水银柱在缩口处断开, 水银柱只能上不能下, 故体温计只能准确测量比原来示数高的体温, 低于原来示数的体温是无法测量的。
10. 某实验小组为探究水的体积随温度变化的关系,进行了如图甲所示的实验:在锥形瓶中装满混有少量红墨水的冷开水,用带细玻璃管的橡皮塞将锥形瓶的瓶口密封,将锥形瓶浸没在水温可设定的热水壶的水中。设置初始温度为40℃,待玻璃管内液面稳定后,用细橡皮筋在液面位置做标记。实验过程中分别设置不同的温度,记录玻璃管内液面稳定后到标记处的距离。
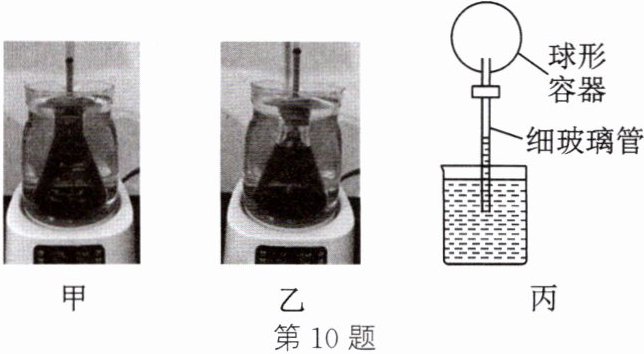
(1)实验中观察锥形瓶内水的体积变化,需要用到的测量仪器是
(2)通过图甲实验,实验小组的同学得到如表所示的数据:
|温度/℃|40|42|44|46|48|50|
|液面到标记处的距离/mm|0|6|11.5|17.5|24|30|
分析数据,可以得出水的体积随温度变化的规律是
(3)在图甲装置的细玻璃管外标上对应的刻度值,可以制成简易的温度计,构成该简易温度计的锥形瓶相当于实验室用普通温度计结构中的
(4)小明同学为了探究空气与水哪个受热后膨胀得更明显,在图甲实验的基础上增加了一组实验:用同一只锥形瓶,在瓶内冷开水上方保留一部分空气(如图乙),重复图甲实验的操作,得到如表所示的数据:
|温度/℃|40|43|45|46|47|49|
|液面到标记处的距离/mm|0|22|37|43.5|52|72|
比较图甲、乙两组实验的数据,可以得出的结论是
(5)图丙为伽利略温度计示意图(球形容器内有空气,细玻璃管内有水),当环境温度升高时,细玻璃管内的液面

(1)实验中观察锥形瓶内水的体积变化,需要用到的测量仪器是
刻度尺
。(2)通过图甲实验,实验小组的同学得到如表所示的数据:
|温度/℃|40|42|44|46|48|50|
|液面到标记处的距离/mm|0|6|11.5|17.5|24|30|
分析数据,可以得出水的体积随温度变化的规律是
当水温高于 40°C 时, 水增大的体积与升高的温度成正比
。(3)在图甲装置的细玻璃管外标上对应的刻度值,可以制成简易的温度计,构成该简易温度计的锥形瓶相当于实验室用普通温度计结构中的
玻璃泡
。(4)小明同学为了探究空气与水哪个受热后膨胀得更明显,在图甲实验的基础上增加了一组实验:用同一只锥形瓶,在瓶内冷开水上方保留一部分空气(如图乙),重复图甲实验的操作,得到如表所示的数据:
|温度/℃|40|43|45|46|47|49|
|液面到标记处的距离/mm|0|22|37|43.5|52|72|
比较图甲、乙两组实验的数据,可以得出的结论是
升高相同温度时, 空气的膨胀程度比水更明显
。(5)图丙为伽利略温度计示意图(球形容器内有空气,细玻璃管内有水),当环境温度升高时,细玻璃管内的液面
下降
,请简述理由:球形容器内气体受热膨胀, 体积变大, 液面下降
(忽略水的体积变化)。这种温度计与现在的液体温度计相比,缺点是不方便携带
(合理即可)。
答案:
(1) 刻度尺
(2) 当水温高于 $ 40^{\circ} \text{C} $ 时, 水增大的体积与升高的温度成正比
(3) 玻璃泡
(4) 升高相同温度时, 空气的膨胀程度比水更明显
(5) 下降 球形容器内气体受热膨胀, 体积变大, 液面下降 不方便携带 (合理即可)
(1) 刻度尺
(2) 当水温高于 $ 40^{\circ} \text{C} $ 时, 水增大的体积与升高的温度成正比
(3) 玻璃泡
(4) 升高相同温度时, 空气的膨胀程度比水更明显
(5) 下降 球形容器内气体受热膨胀, 体积变大, 液面下降 不方便携带 (合理即可)
查看更多完整答案,请扫码查看


