《2025年暑期升级训练浙江教育出版社七年级科学浙教版》

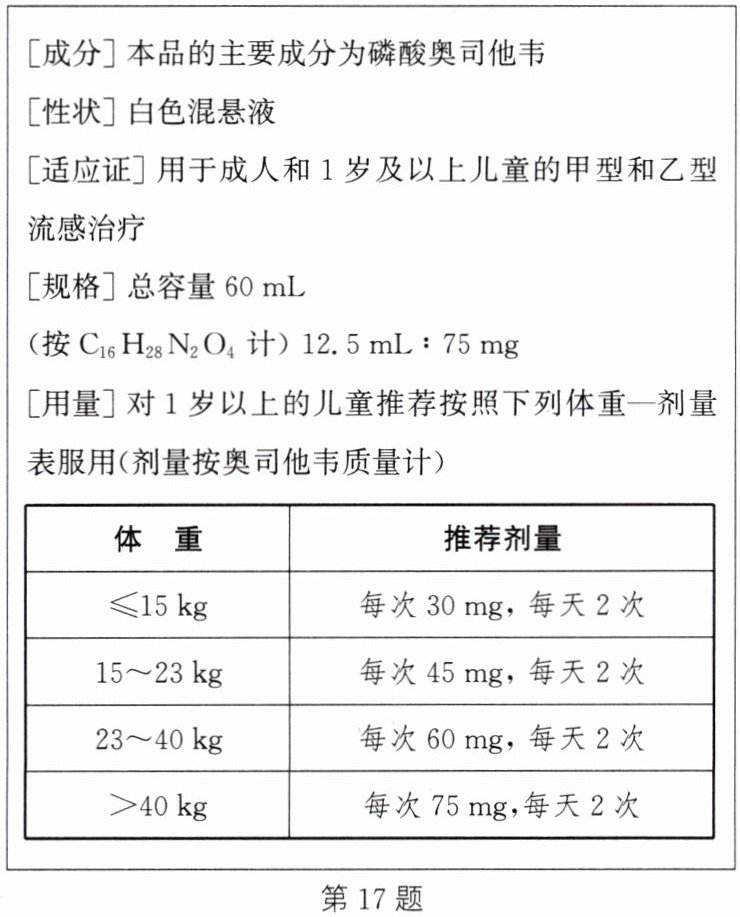
17. (11分)浙江省疾控中心提醒,春季流感高发,注意防控。如果被确诊为甲流,医生建议在48小时内服用磷酸奥司他韦,可以有效缩短病程。如图所示为磷酸奥司他韦干混悬剂说明书的部分内容。

(1)奥司他韦分子中碳、氧原子的个数比为______4:1。
(2)奥司他韦$(C_1_6H_2_8N_2O_4)$中氮元素的质量分数是______9%。(结果精确到1%)
(3)某甲流患者的体重是25kg,在治疗过程中,他需每天服用奥司他韦2次,那么该患者每天需服用该混悬剂多少毫升？(请写出计算过程)
解：某甲流患者的体重是25 kg，每次 60 mg，每天两次，那么该患者每天需服用该混悬剂的体积为 12.5 mL× $\frac{60 mg×2}{75 mg}$ = 20 mL

答案：
(1) 4:1
(2) 9%
(3) 某甲流患者的体重是 25 kg，每次 60 mg，每天两次，那么该患者每天需服用该混悬剂的体积为 12.5 mL× $\frac{60 mg×2}{75 mg}$ = 20 mL

18. (15分)小明看见爷爷买了两个健身铁球,时常拿在手里转来转去,他一直想知道这两个铁球是实心的还是空心的。当他学完密度的知识后,利用了家里的电子秤和杯子做了以下实验进行判断,步骤如下：他选了一个铁球进行测量,找一个能够把铁球浸没的装满水的容器后,用电子秤测出水和容器的总质量m₀为1.5kg,再测出这个铁球的质量$m_1$为0.79kg,将这个铁球轻轻地放进装满水的容器里直到浸没,待水不再溢出后,测得铁球、剩余水和容器的总质量$m_2$为2.14kg。(已知ρ铁$= 7.9×10^3kg/m^3,ρ$水$= 1.0×10^3kg/m^3,ρ$铝$= 2.7×10^3kg/m^3)$
(1)请判断铁球是实心的还是空心的,并写出判断依据。
铁球是空心的。判断依据：溢出水的质量 m_{溢}=m₀ + m₁ - m₂ = 1.5 kg + 0.79 kg - 2.14 kg = 0.15 kg，由 ρ= $\frac{m}{V}$ 可得，溢出水的体积 V_{溢}= $\frac{m_{溢}}{ρ_{水}}$ = $\frac{0.15 kg}{1.0×10³ kg/m³}$ = 1.5×10⁻⁴ m³，由于铁球浸没在容器里，所以铁球的体积 V = V_{溢}=1.5×10⁻⁴ m³，铁球中铁的体积 V_{铁}= $\frac{m₁}{ρ_{铁}}$ = $\frac{0.79 kg}{7.9×10³ kg/m³}$ = 1.0×10⁻⁴ m³，由此可知，V_{铁} ＜ V，因此铁球是空心的
(2)如果铁球是空心的,那么空心部分的体积有多大？
5.0×10⁻⁵ m³
(3)如果制作铁球时在其空心部分注满铝,那么该球的总质量是多少？
0.925 kg

答案：
(1) 溢出水的质量 m_{溢}=m₀ + m₁ - m₂ = 1.5 kg + 0.79 kg - 2.14 kg = 0.15 kg，由 ρ= $\frac{m}{V}$ 可得，溢出水的体积 V_{溢}= $\frac{m_{溢}}{ρ_{水}}$ = $\frac{0.15 kg}{1.0×10³ kg/m³}$ = 1.5×10⁻⁴ m³，由于铁球浸没在容器里，所以铁球的体积 V = V_{溢}=1.5×10⁻⁴ m³，铁球中铁的体积 V_{铁}= $\frac{m₁}{ρ_{铁}}$ = $\frac{0.79 kg}{7.9×10³ kg/m³}$ = 1.0×10⁻⁴ m³，由此可知，V_{铁} ＜ V，因此铁球是空心的
(2) 空心部分的体积 V_{空}=V - V_{铁}=1.5×10⁻⁴ m³ - 1.0×10⁻⁴ m³ = 5.0×10⁻⁵ m³
(3) 若空心部分注满铝，则 V_{铝}=V_{空}=5.0×10⁻⁵ m³，铝的质量 m_{铝}=ρ_{铝}V_{铝}=2.7×10³ kg/m³×5.0×10⁻⁵ m³ = 0.135 kg，此时该球的总质量 m_{总}=m₁ + m_{铝}=0.79 kg + 0.135 kg = 0.925 kg