《2025年智趣夏令营玩转数学五年级通用版》

5. 计算下面各题。
$\frac {7}{18}+\frac {5}{18}-\frac {3}{18}$ $1-\frac {1}{3}-\frac {2}{9}$ $(\frac {1}{2}+\frac {1}{4})+\frac {1}{5}$
$\frac {3}{5}-\frac {1}{10}-\frac {2}{15}$ $\frac {3}{4}+\frac {4}{5}+\frac {3}{5}$ $\frac {3}{2}-(\frac {6}{7}-\frac {1}{6})$

答案： 【解析】：
1. 对于$\frac{7}{18}+\frac{5}{18}-\frac{3}{18}$：
同分母分数相加减，分母不变，分子相加减。所以$\frac{7}{18}+\frac{5}{18}-\frac{3}{18}=\frac{7 + 5-3}{18}=\frac{9}{18}=\frac{1}{2}$。
2. 对于$1-\frac{1}{3}-\frac{2}{9}$：
先把$1$化为分母是$9$的分数，$1=\frac{9}{9}$，$\frac{1}{3}=\frac{3}{9}$。
则$1-\frac{1}{3}-\frac{2}{9}=\frac{9}{9}-\frac{3}{9}-\frac{2}{9}=\frac{9 - 3-2}{9}=\frac{4}{9}$。
3. 对于$(\frac{1}{2}+\frac{1}{4})+\frac{1}{5}$：
先计算括号内的$\frac{1}{2}+\frac{1}{4}$，通分，$\frac{1}{2}=\frac{2}{4}$，则$\frac{1}{2}+\frac{1}{4}=\frac{2 + 1}{4}=\frac{3}{4}$。
再计算$\frac{3}{4}+\frac{1}{5}$，通分，$\frac{3}{4}=\frac{15}{20}$，$\frac{1}{5}=\frac{4}{20}$，所以$\frac{3}{4}+\frac{1}{5}=\frac{15+4}{20}=\frac{19}{20}$。
4. 对于$\frac{3}{5}-\frac{1}{10}-\frac{2}{15}$：
先通分，$5$、$10$、$15$的最小公倍数是$30$，$\frac{3}{5}=\frac{18}{30}$，$\frac{1}{10}=\frac{3}{30}$，$\frac{2}{15}=\frac{4}{30}$。
则$\frac{3}{5}-\frac{1}{10}-\frac{2}{15}=\frac{18}{30}-\frac{3}{30}-\frac{4}{30}=\frac{18 - 3-4}{30}=\frac{11}{30}$。
5. 对于$\frac{3}{4}+\frac{4}{5}+\frac{3}{5}$：
根据加法结合律$a + b + c=a+(b + c)$，先计算$\frac{4}{5}+\frac{3}{5}=\frac{4 + 3}{5}=\frac{7}{5}$。
再计算$\frac{3}{4}+\frac{7}{5}$，通分，$\frac{3}{4}=\frac{15}{20}$，$\frac{7}{5}=\frac{28}{20}$，所以$\frac{3}{4}+\frac{4}{5}+\frac{3}{5}=\frac{15+28}{20}=\frac{43}{20}$。
6. 对于$\frac{3}{2}-(\frac{6}{7}-\frac{1}{6})$：
先计算括号内的$\frac{6}{7}-\frac{1}{6}$，通分，$\frac{6}{7}=\frac{36}{42}$，$\frac{1}{6}=\frac{7}{42}$，则$\frac{6}{7}-\frac{1}{6}=\frac{36 - 7}{42}=\frac{29}{42}$。
再计算$\frac{3}{2}-\frac{29}{42}$，通分，$\frac{3}{2}=\frac{63}{42}$，所以$\frac{3}{2}-(\frac{6}{7}-\frac{1}{6})=\frac{63}{42}-\frac{29}{42}=\frac{63 - 29}{42}=\frac{34}{42}=\frac{17}{21}$。
【答案】：$\frac{1}{2}$；$\frac{4}{9}$；$\frac{19}{20}$；$\frac{11}{30}$；$\frac{43}{20}$；$\frac{17}{21}$

6. 解方程。
$\frac {7}{9}+x=1$，$x=$$\frac{2}{9}$
$x-\frac {13}{15}=\frac {19}{30}$，$x=$$\frac{3}{2}$
$\frac {5}{7}-x=\frac {1}{14}$，$x=$$\frac{9}{14}$

答案： 【解析】：
1. 对于方程$\frac{7}{9}+x = 1$：
根据等式的性质，等式两边同时减去一个数，等式仍然成立。为了求出$x$的值，在方程两边同时减去$\frac{7}{9}$，即$x=1 - \frac{7}{9}$。
把$1$转化为$\frac{9}{9}$，则$x=\frac{9}{9}-\frac{7}{9}=\frac{9 - 7}{9}=\frac{2}{9}$。
2. 对于方程$x-\frac{13}{15}=\frac{19}{30}$：
根据等式的性质，等式两边同时加上一个数，等式仍然成立。在方程两边同时加上$\frac{13}{15}$，得到$x=\frac{19}{30}+\frac{13}{15}$。
先对$\frac{13}{15}$进行通分，$\frac{13}{15}=\frac{13\times2}{15\times2}=\frac{26}{30}$，则$x=\frac{19}{30}+\frac{26}{30}=\frac{19 + 26}{30}=\frac{45}{30}$，约分后$x=\frac{3}{2}$。
3. 对于方程$\frac{5}{7}-x=\frac{1}{14}$：
首先根据等式的性质，在方程两边同时加上$x$，得到$\frac{5}{7}=\frac{1}{14}+x$。
然后再根据等式的性质，在方程两边同时减去$\frac{1}{14}$，即$x=\frac{5}{7}-\frac{1}{14}$。
对$\frac{5}{7}$进行通分，$\frac{5}{7}=\frac{5\times2}{7\times2}=\frac{10}{14}$，则$x=\frac{10}{14}-\frac{1}{14}=\frac{10 - 1}{14}=\frac{9}{14}$。
【答案】：$x=\frac{2}{9}$；$x=\frac{3}{2}$；$x=\frac{9}{14}$

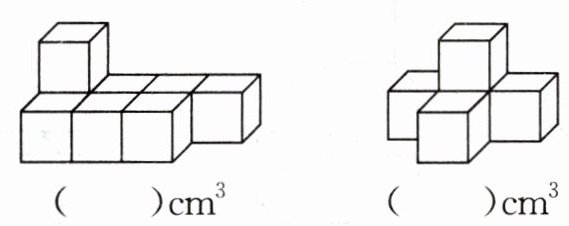
7. 下面的图形都是用棱长 1cm 的正方体拼成的,它们的体积分别是多少?

（8$cm^{3}$）、（5$cm^{3}$）

答案： 【解析】：
第一个图形：通过数小正方体的个数，第一层有$7$个，第二层有$1$个，一共有$7 + 1=8$个小正方体。因为每个小正方体体积是$1\times1\times1 = 1cm^{3}$，所以该图形体积是$8\times1 = 8cm^{3}$。
第二个图形：数小正方体个数，第一层有$4$个，第二层有$1$个，一共有$4+1 = 5$个小正方体。每个小正方体体积$1cm^{3}$，所以该图形体积是$5\times1=5cm^{3}$。
【答案】：$8$；$5$

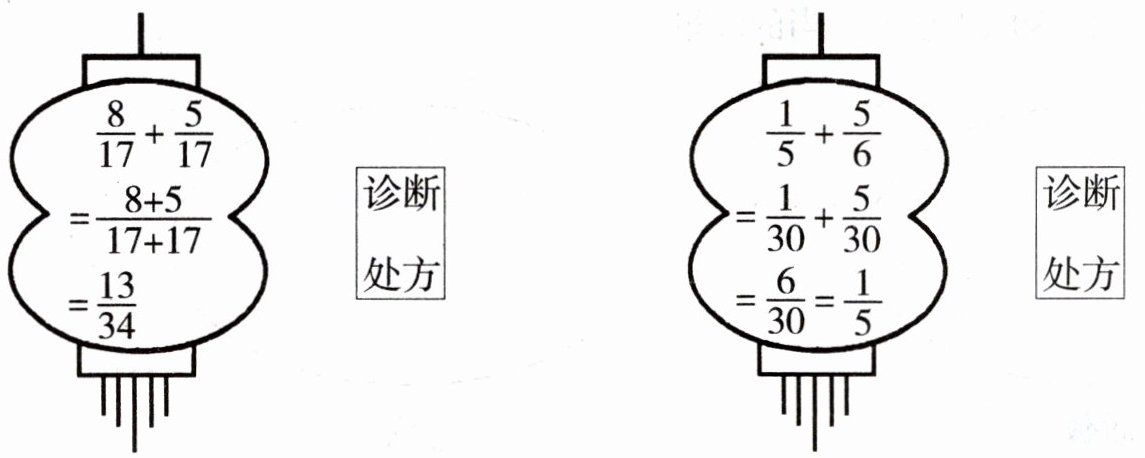
8. 名医门诊。

- 第一个式子：
$\begin{aligned}\frac{8}{17}+\frac{5}{17}&=\frac{8 + 5}{17}\\&=\frac{13}{17}\end{aligned}$
- 第二个式子：
$\begin{aligned}\frac{1}{5}+\frac{5}{6}&=\frac{6}{30}+\frac{25}{30}\\&=\frac{6 + 25}{30}\\&=\frac{31}{30}\end{aligned}$

答案： 【解析】：
- 第一个式子：同分母分数相加，分母不变，分子相加。原计算错误地将分母也相加了。
- 第二个式子：异分母分数相加，应先通分，找到$5$和$6$的最小公倍数$30$，将$\frac{1}{5}$化为$\frac{6}{30}$，$\frac{5}{6}$化为$\frac{25}{30}$，再相加。原计算在通分过程中分子计算错误。
【答案】：
- 第一个式子：
$\begin{aligned}\frac{8}{17}+\frac{5}{17}&=\frac{8 + 5}{17}\\&=\frac{13}{17}\end{aligned}$
- 第二个式子：
$\begin{aligned}\frac{1}{5}+\frac{5}{6}&=\frac{6}{30}+\frac{25}{30}\\&=\frac{6 + 25}{30}\\&=\frac{31}{30}\end{aligned}$