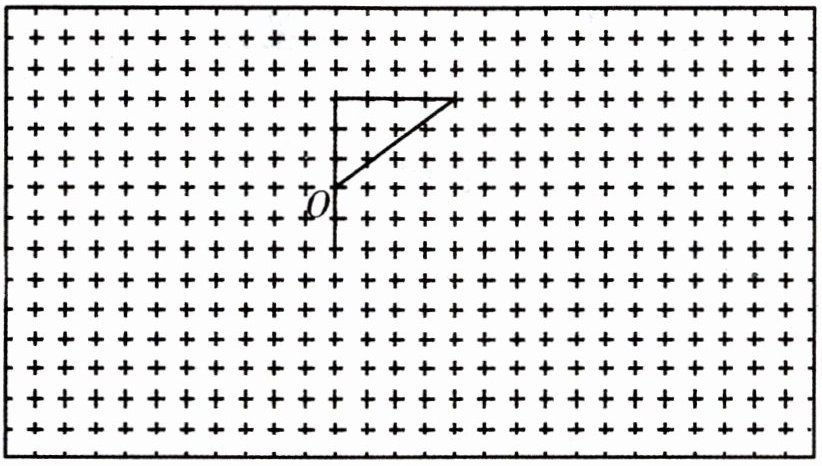
3. 利用旋转画一个风车,并涂上颜色。

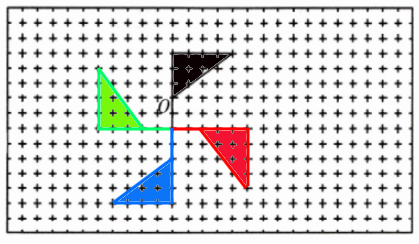
答案:

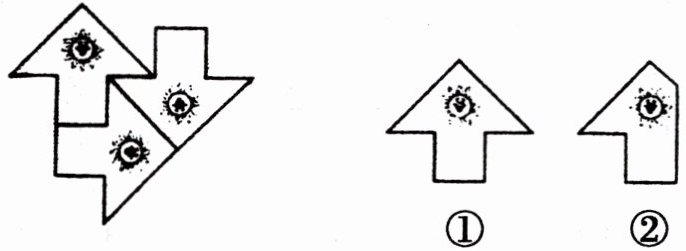
4. 下图是由哪个图形平移或旋转而成的,你能在右边两幅图中圈出来吗?
(圈

(圈
①
)
答案:
【解析】:通过观察图形的形状、大小和图案分布等特征,判断是由哪个基本图形通过平移或旋转得到的。左边的复杂图形可以看作是由右边图①通过平移和旋转组合而成。
【答案】:圈①
【答案】:圈①
5. 下面哪些图案由图形①旋转可以得到?在下面括号中画“√”。

( )(

( )(
√
)( )(√
)
答案:
( )(√)( )(√)
6. 解方程。
$x-\frac {2}{7}=\frac {5}{6}$,$x=$
$\frac {9}{11}-x=\frac {3}{22}$,$x=$
$\frac {4}{5}+x=1$,$x=$
$x-\frac {2}{7}=\frac {5}{6}$,$x=$
$\frac{47}{42}$
$\frac {9}{11}-x=\frac {3}{22}$,$x=$
$\frac{15}{22}$
$\frac {4}{5}+x=1$,$x=$
$\frac{1}{5}$
答案:
【解析】:
对于方程$x - \frac{2}{7}=\frac{5}{6}$,根据等式的性质,等式两边同时加上相同的数,等式仍然成立。在方程两边同时加上$\frac{2}{7}$,则$x=\frac{5}{6}+\frac{2}{7}$,通分可得$x = \frac{35}{42}+\frac{12}{42}=\frac{35 + 12}{42}=\frac{47}{42}$。
对于方程$\frac{9}{11}-x=\frac{3}{22}$,根据等式的性质,先在等式两边同时加上$x$,得到$\frac{9}{11}=\frac{3}{22}+x$,再在等式两边同时减去$\frac{3}{22}$,则$x=\frac{9}{11}-\frac{3}{22}$,通分可得$x=\frac{18}{22}-\frac{3}{22}=\frac{18 - 3}{22}=\frac{15}{22}$。
对于方程$\frac{4}{5}+x = 1$,根据等式的性质,等式两边同时减去$\frac{4}{5}$,则$x=1-\frac{4}{5}=\frac{5}{5}-\frac{4}{5}=\frac{5 - 4}{5}=\frac{1}{5}$。
【答案】:$x=\frac{47}{42}$;$x=\frac{15}{22}$;$x=\frac{1}{5}$
对于方程$x - \frac{2}{7}=\frac{5}{6}$,根据等式的性质,等式两边同时加上相同的数,等式仍然成立。在方程两边同时加上$\frac{2}{7}$,则$x=\frac{5}{6}+\frac{2}{7}$,通分可得$x = \frac{35}{42}+\frac{12}{42}=\frac{35 + 12}{42}=\frac{47}{42}$。
对于方程$\frac{9}{11}-x=\frac{3}{22}$,根据等式的性质,先在等式两边同时加上$x$,得到$\frac{9}{11}=\frac{3}{22}+x$,再在等式两边同时减去$\frac{3}{22}$,则$x=\frac{9}{11}-\frac{3}{22}$,通分可得$x=\frac{18}{22}-\frac{3}{22}=\frac{18 - 3}{22}=\frac{15}{22}$。
对于方程$\frac{4}{5}+x = 1$,根据等式的性质,等式两边同时减去$\frac{4}{5}$,则$x=1-\frac{4}{5}=\frac{5}{5}-\frac{4}{5}=\frac{5 - 4}{5}=\frac{1}{5}$。
【答案】:$x=\frac{47}{42}$;$x=\frac{15}{22}$;$x=\frac{1}{5}$
查看更多完整答案,请扫码查看


