《2025年智趣夏令营玩转数学五年级通用版》

3. 解方程。
$\frac {2}{3}+x=\frac {7}{9}$，解得$x=$$\frac{1}{9}$
$\frac {1}{15}+x=\frac {2}{3}$，解得$x=$$\frac{3}{5}$
$\frac {7}{8}-x=\frac {1}{4}$，解得$x=$$\frac{5}{8}$

答案： 【解析】：
1. 对于方程$\frac{2}{3}+x = \frac{7}{9}$：
根据等式的性质，等式两边同时减去一个数，等式仍然成立。为了求出$x$的值，在等式两边同时减去$\frac{2}{3}$，则$x=\frac{7}{9}-\frac{2}{3}$。
先将$\frac{2}{3}$通分，$\frac{2}{3}=\frac{2\times3}{3\times3}=\frac{6}{9}$，所以$x = \frac{7}{9}-\frac{6}{9}=\frac{7 - 6}{9}=\frac{1}{9}$。
2. 对于方程$\frac{1}{15}+x=\frac{2}{3}$：
同样根据等式的性质，在等式两边同时减去$\frac{1}{15}$，得到$x=\frac{2}{3}-\frac{1}{15}$。
对$\frac{2}{3}$通分，$\frac{2}{3}=\frac{2\times5}{3\times5}=\frac{10}{15}$，则$x=\frac{10}{15}-\frac{1}{15}=\frac{10 - 1}{15}=\frac{9}{15}=\frac{3}{5}$。
3. 对于方程$\frac{7}{8}-x=\frac{1}{4}$：
首先根据等式的性质，在等式两边同时加上$x$，得到$\frac{7}{8}=\frac{1}{4}+x$。
然后再在等式两边同时减去$\frac{1}{4}$，即$x=\frac{7}{8}-\frac{1}{4}$。
对$\frac{1}{4}$通分，$\frac{1}{4}=\frac{1\times2}{4\times2}=\frac{2}{8}$，所以$x=\frac{7}{8}-\frac{2}{8}=\frac{7 - 2}{8}=\frac{5}{8}$。
【答案】：$x=\frac{1}{9}$；$x = \frac{3}{5}$；$x=\frac{5}{8}$

4. 下面的图案分别是由哪个图形旋转而成的？把这个图形画在横线上。

答案：

红框框中的部分旋转形成的

5. 小明、小立和小春赛跑。同样距离小明用了$5\frac {3}{5}$分钟,小立用了$5\frac {5}{6}$分钟,小春用了$5\frac {4}{7}$分钟。冠、亚、季军分别是谁？请把他们送上领奖台。

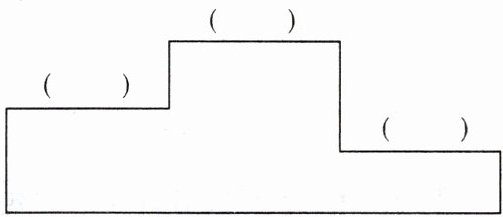
领奖台从左到右依次填：小明、小春、小立。

答案： 【解析】：比较$5\frac{3}{5}$、$5\frac{5}{6}$、$5\frac{4}{7}$的大小。
先比较整数部分，都是$5$，相同。
再比较分数部分：
$\frac{3}{5}=\frac{3\times42}{5\times42}=\frac{126}{210}$
$\frac{5}{6}=\frac{5\times35}{6\times35}=\frac{175}{210}$
$\frac{4}{7}=\frac{4\times30}{7\times30}=\frac{120}{210}$
因为$\frac{120}{210}＜\frac{126}{210}＜\frac{175}{210}$，即$\frac{4}{7}＜\frac{3}{5}＜\frac{5}{6}$。
所以$5\frac{4}{7}＜5\frac{3}{5}＜5\frac{5}{6}$。
赛跑比赛用时短的跑得快。
【答案】：冠军是小春，亚军是小明，季军是小立。领奖台从左到右依次填：小明、小春、小立。

6. 学校要在墙上建一个长方体的橱窗,用来展示好人好事。橱窗长 3m,宽 20cm,高 80cm。现要在四周安上角铁(靠墙面的四边不安角铁),至少需要多长角铁?

答案： 8.4m