《2025年文涛书业假期作业快乐暑假七年级数学北师大版》

11. 若$a + b = - 4$,$ab = - 1$,则$a^{2} + b^{2} =$18.

答案： 11. 18

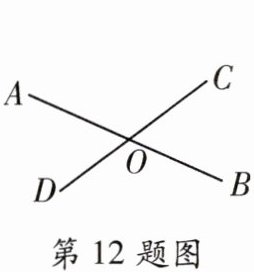
12. 如图,已知直线$AB$、$CD$相交于点$O$,$∠AOC + ∠BOD = 210^{\circ}$,则$∠BOC =$$75^{\circ}$.

答案： 12. $75^{\circ}$

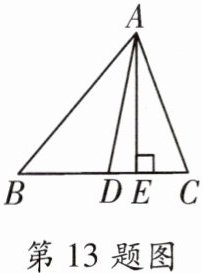
13. 如图,$AD$、$AE$分别是$△ABC$的角平分线和高线,且$∠B = 50^{\circ}$,$∠C = 70^{\circ}$,则$∠EAD =$$10^{\circ}$.

答案： 13. $10^{\circ}$

14. 先化简,再求值:
(1)$(4ab^{3} - 8a^{2}b^{2})÷4ab + (2a + b)\cdot(2a - b)$,其中$a = 2$,$b = 1$,值为12;
(2)已知$a$、$b$满足$b - a = - 2023$,求代数式$[(a + b)(a - b) - (a - b)^{2} - 2b(b - a)]÷4b$的值为2023.

答案： 14. 解：
(1) 原式 $=b^{2}-2ab+4a^{2}-b^{2}=4a^{2}-2ab$，将 $a=2$，$b=1$ 代入得 $4×2^{2}-2×2×1=12$。
(2) 原式 $=[a^{2}-b^{2}-(a^{2}+b^{2}-2ab)-2b^{2}+2ab]÷4b$
$=[a^{2}-b^{2}-a^{2}-b^{2}+2ab-2b^{2}+2ab]÷4b$
$=(4ab-4b^{2})÷4b$
$=a-b$，
$\because b-a=-2023$，
$\therefore a-b=-(b-a)=2023$

15. 如图,在$△ABC$中,$AB = AC$,$BD = CD$,$DE⊥AB$,$DF⊥AC$,垂足分别为点$E$、$F$.试说明:$△BED≌△CFD$.
解：$\because DE⊥AB$，$DF⊥AC$，
$\therefore ∠BED=∠CFD=90^{\circ}$。
$\because AB=AC$，$\therefore ∠B=∠C$。
在 $\triangle BED$ 和 $\triangle CFD$ 中，$\begin{cases}∠DEB=∠DFC,\\∠B=∠C,\\BD=CD,\end{cases}$
$\therefore \triangle BED≌\triangle CFD$(AAS)。

答案： 15. 解：$\because DE⊥AB$，$DF⊥AC$，
$\therefore ∠BED=∠CFD=90^{\circ}$。
$\because AB=AC$，$\therefore ∠B=∠C$。
在 $\triangle BED$ 和 $\triangle CFD$ 中，$\begin{cases}∠DEB=∠DFC,\\∠B=∠C,\\BD=CD,\end{cases}$
$\therefore \triangle BED≌\triangle CFD(AAS)$。