2025年文涛书业假期作业快乐暑假七年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年文涛书业假期作业快乐暑假七年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列运算正确的是 (
A. $ a - 2a = a $
B. $ (-a^{2})^{3} = -a^{6} $
C. $ x^{6} \div x^{3} = x^{2} $
D. $ (x + y)^{2} = x^{2} + y^{2} $
B
)A. $ a - 2a = a $
B. $ (-a^{2})^{3} = -a^{6} $
C. $ x^{6} \div x^{3} = x^{2} $
D. $ (x + y)^{2} = x^{2} + y^{2} $
答案:
B
2. 若 $ a + b = 3 $,$ a - b = 7 $,则 $ ab = $ (
A. -10
B. -40
C. 10
D. 40
A
)A. -10
B. -40
C. 10
D. 40
答案:
A
3. 下列条件中,能判定 $ \triangle ABC $ 为直角三角形的是 (
A. $ \angle A = \angle B = \angle C $
B. $ \angle A + \angle B = 2\angle C $
C. $ \angle A : \angle B : \angle C = 1 : 2 : 3 $
D. $ \angle A = \frac{1}{2}\angle B = \frac{1}{2}\angle C $
C
)A. $ \angle A = \angle B = \angle C $
B. $ \angle A + \angle B = 2\angle C $
C. $ \angle A : \angle B : \angle C = 1 : 2 : 3 $
D. $ \angle A = \frac{1}{2}\angle B = \frac{1}{2}\angle C $
答案:
C
4. 一个等腰三角形的两边长分别是 3 和 7,则它的周长为 (
A. 17
B. 15
C. 13
D. 13 或 17
A
)A. 17
B. 15
C. 13
D. 13 或 17
答案:
A
5. 如图,$ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ AC = 3 $,点 $ P $ 是边 $ BC $ 上的动点,则 $ AP $ 长不可能是 (
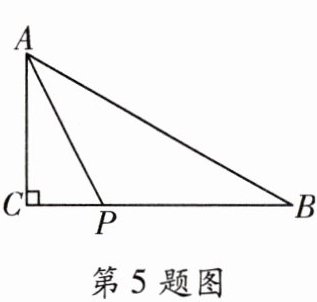
A. 2.5
B. 3
C. 4
D. 5
A
)
A. 2.5
B. 3
C. 4
D. 5
答案:
A
6. 如图,直线 $ a // b $,一个含 $ 60^{\circ} $ 角的直角三角板 $ ABC(\angle A = 60^{\circ}) $ 按如图所示位置,若 $ \angle 1 = 55^{\circ} $,则 $ \angle 2 $ 的度数为 (
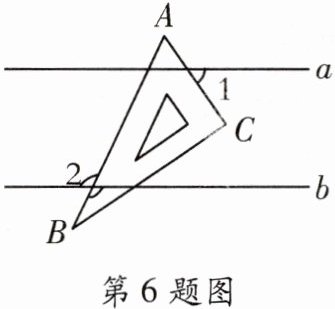
A. $ 105^{\circ} $
B. $ 110^{\circ} $
C. $ 115^{\circ} $
D. $ 120^{\circ} $
C
)
A. $ 105^{\circ} $
B. $ 110^{\circ} $
C. $ 115^{\circ} $
D. $ 120^{\circ} $
答案:
C
7. 在 10 个外观相同的产品中,有 2 个不合格产品,现从中任意抽取 1 个进行检测,抽到不合格产品的概率是 (
A. $ \frac{1}{10} $
B. $ \frac{1}{5} $
C. $ \frac{2}{5} $
D. $ \frac{4}{5} $
B
)A. $ \frac{1}{10} $
B. $ \frac{1}{5} $
C. $ \frac{2}{5} $
D. $ \frac{4}{5} $
答案:
B
8. 如图,$ l_{1} // l_{1} $,则 $ \angle ADC $ 的度数为 (

A. $ 90^{\circ} $
B. $ 95^{\circ} $
C. $ 85^{\circ} $
D. $ 80^{\circ} $
B
)
A. $ 90^{\circ} $
B. $ 95^{\circ} $
C. $ 85^{\circ} $
D. $ 80^{\circ} $
答案:
B
9. 如图,$ \triangle ABC $ 中,$ AC = 5 $,$ DE $ 垂直平分 $ BC $,若 $ \triangle AEC $ 的周长为 12,则 $ AB $ 长为 (
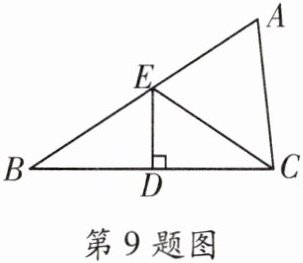
A. 5
B. 6
C. 7
D. 8
C
)
A. 5
B. 6
C. 7
D. 8
答案:
C
10. 已知 $ 10^{x} = m $,$ 10^{y} = n $,则 $ 10^{2x + 3y} = $
$m ^ { 2 } n ^ { 3 }$
.
答案:
$m ^ { 2 } n ^ { 3 }$
11. 如图,$ AB = AC $,$ \angle A = 100^{\circ} $,$ AB // CD $,则 $ \angle BCD = $

$40^{\circ}$
.
答案:
$40 ^ { \circ }$
12. 如图,$ \angle C = 90^{\circ} $,$ BD $ 是 $ \angle ABC $ 的平分线,$ DE $ 是 $ AB $ 的垂直平分线,则 $ \angle A = $
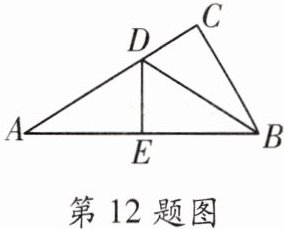
$30^{\circ}$
.
答案:
$30 ^ { \circ }$
13. 已知 $ (a + b)^{2} = 25 $,$ (a - b)^{2} = 9 $,求 $ ab $ 与 $ a^{2} + b^{2} $ 的值.
$ ab = $
$ ab = $
4
,$ a^{2} + b^{2} = $17
.
答案:
解:$\because ( a + b ) ^ { 2 } = 25$,$( a - b ) ^ { 2 } = 9$,
$\therefore a ^ { 2 } + 2 a b + b ^ { 2 } = 25$,①
$a ^ { 2 } - 2 a b + b ^ { 2 } = 9$。②
$\therefore$ ① - ②,得 $4 a b = 16$,$\therefore a b = 4$。
① + ②,得 $2 a ^ { 2 } + 2 b ^ { 2 } = 34$,$\therefore a ^ { 2 } + b ^ { 2 } = 17$。
$\therefore a ^ { 2 } + 2 a b + b ^ { 2 } = 25$,①
$a ^ { 2 } - 2 a b + b ^ { 2 } = 9$。②
$\therefore$ ① - ②,得 $4 a b = 16$,$\therefore a b = 4$。
① + ②,得 $2 a ^ { 2 } + 2 b ^ { 2 } = 34$,$\therefore a ^ { 2 } + b ^ { 2 } = 17$。
查看更多完整答案,请扫码查看


