《2025年文涛书业假期作业快乐暑假七年级数学北师大版》

12. 某游泳池中有水 $ 600 \mathrm{~m}^{3} $，每小时注入水 $ 50 \mathrm{~m}^{3} $，则游泳池内水的体积 $ Q $（$ \mathrm{m}^{3} $）随时间 $ t $（小时）的变化而变化，则 $ Q $ 与 $ t $ 的关系式为$ Q = 50 t + 600 $.

答案： $ Q = 50 t + 600 $

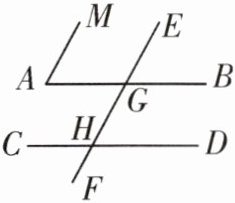
13. 如图，$ \angle A = 70^{\circ} $，$ \angle BGE = 70^{\circ} $，$ \angle CHG = 110^{\circ} $，试说明：
(1) $ AM // EF $；
(2) $ AB // CD $.

(1) 解：$ \because \angle A = 70 ^ { \circ } $，$ \angle B G E = 70 ^ { \circ } $，
$ \therefore \angle A = \angle B G E $，$ \therefore AM // EF $（同位角相等，两直线平行）。
(2) 解：$ \because \angle C H G = 110 ^ { \circ } $，$ \angle C H G + \angle G H D = 180 ^ { \circ } $（邻补角的定义），
$ \therefore \angle G H D = 180 ^ { \circ } - 110 ^ { \circ } = 70 ^ { \circ } $，
又 $ \because \angle B G E = 70 ^ { \circ } $，$ \therefore \angle B G E = \angle G H D $，
$ \therefore AB // CD $（同位角相等，两直线平行）。

答案： 解：
(1) $ \because \angle A = 70 ^ { \circ } $，$ \angle B G E = 70 ^ { \circ } $，
$ \therefore \angle A = \angle B G E $，$ \therefore A M // E F $。
(2) $ \because \angle C H G = 110 ^ { \circ } $，$ \angle C H G + \angle G H D = 180 ^ { \circ } $，
$ \therefore \angle G H D = 180 ^ { \circ } - 110 ^ { \circ } = 70 ^ { \circ } $，
又 $ \because \angle B G E = 70 ^ { \circ } $，$ \therefore \angle B G E = \angle G H D $，
$ \therefore A B // C D $。

14. 如图，$ \triangle ABC $ 是边长为 $ 6 \mathrm{~cm} $ 的等边三角形，$ BD $ 是中线，延长 $ BC $ 至 $ E $ 点，使 $ CE = CD $.

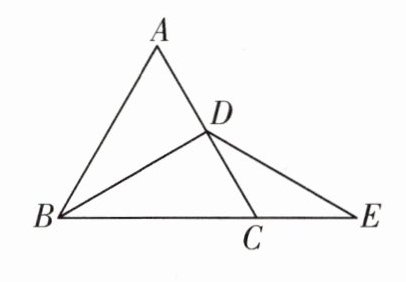
(1) 求 $ CE $ 的长；3cm
(2) 求 $ \angle E $ 的度数.30°

答案： 解：
(1) $ \because \triangle A B C $ 是边长为 $ 6 \mathrm { cm } $ 的等边三角形，$ B D $ 是中线，
$ \therefore A D = C D = \frac { 1 } { 2 } A C = \frac { 1 } { 2 } \times 6 = 3 ( \mathrm { cm } ) $。
又 $ \because C E = C D $，$ \therefore C E = 3 ( \mathrm { cm } ) $；
(2) $ \because \triangle A B C $ 是边长为 $ 6 \mathrm { cm } $ 的等边三角形，
$ \therefore \angle A C E = \angle A + \angle A B C = 60 ^ { \circ } + 60 ^ { \circ } = 120 ^ { \circ } $。
$ \because C E = C D $，
$ \therefore \angle C D E = \angle E = \frac { 180 ^ { \circ } - 120 ^ { \circ } } { 2 } = 30 ^ { \circ } $。