《2025年文涛书业假期作业快乐暑假七年级数学北师大版》

12. 已知$6m^{4}n^{x}÷2m^{y}n^{2}=3mn$,求$x^{y}$的值.

答案： 解：$ 6 m ^ { 4 } n ^ { x } \div 2 m ^ { y } n ^ { 2 } = 3 m ^ { 4 - y } n ^ { x - 2 } = 3 m n $。
故$ \left\{ \begin{array} { l } { 4 - y = 1, } \\ { x - 2 = 1. } \end{array} \right. $即$ \left\{ \begin{array} { l } { x = 3, } \\ { y = 3. } \end{array} \right. $所以$ x ^ { y } = 3 ^ { 3 } = 27 $。

13. 如图,点E,A,C在同一直线上,$AB// CD,AB=CE,AC=CD$. 求证:$BC=ED$.
证明：$ \because A B // C D $，$ \therefore $$\angle B A C = \angle E C D$，
在$ \triangle A B C $和$ \triangle C E D $中，$ \left\{ \begin{array} { l } { A B = C E, } \\ { \angle B A C = \angle E C D, } \\ { A C = C D, } \end{array} \right. $
$ \therefore $$\triangle A B C \cong \triangle C E D$，$ \therefore B C = E D $。

答案： 证明：$ \because A B // C D $，$ \therefore \angle B A C = \angle E C D $，
在$ \triangle A B C $和$ \triangle C E D $中，$ \left\{ \begin{array} { l } { A B = C E, } \\ { \angle B A C = \angle E C D, } \\ { A C = C D, } \end{array} \right. $
$ \therefore \triangle A B C \cong \triangle C E D $，$ \therefore B C = E D $。

14. 如图,在$△ABC$中,$AB=AD=DC,∠BAD=26^{\circ }$,求$∠C$的度数.

解：在$ \triangle A B D $中，$ A B = A D $，
$ \therefore \angle B = \angle A D B = ( 180 ^ { \circ } - 26 ^ { \circ } ) × \frac { 1 } { 2 } = 77 ^ { \circ } $，
$ \therefore \angle A D C = 180 ^ { \circ } - 77 ^ { \circ } = 103 ^ { \circ } $。
在$ \triangle A D C $中，$ A D = D C $，
$ \therefore \angle C = \frac { 1 } { 2 } × ( 180 ^ { \circ } - 103 ^ { \circ } ) = \frac { 1 } { 2 } × 77 ^ { \circ } = 38.5^{\circ} $。

答案： 解：在$ \triangle A B D $中，$ A B = A D $，
$ \therefore \angle B = \angle A D B = ( 180 ^ { \circ } - 26 ^ { \circ } ) \times \frac { 1 } { 2 } = 77 ^ { \circ } $，
$ \therefore \angle A D C = 180 ^ { \circ } - 77 ^ { \circ } = 103 ^ { \circ } $。
在$ \triangle A D C $中，$ A D = D C $，
$ \therefore \angle C = \frac { 1 } { 2 } \times ( 180 ^ { \circ } - 103 ^ { \circ } ) = \frac { 1 } { 2 } \times 77 ^ { \circ } = 38.5 ^ { \circ } $。

15. 如图,$△ABC$中,$AB=AC$,AD是BC边上的中线,$AE// BC,CE⊥AE$,垂足为E. 求证:$△ABD\cong △CAE$.
证明：$ \because A B = A C $，$ \therefore \angle B = \angle A C B $。
$ \because A D $是$ B C $边上的中线，
$ \therefore $AD⊥BC，即$ \angle A D B = 90 ^ { \circ } $。
$ \because A E // B C $，$ \therefore $∠EAC=∠ACB。
$ \therefore \angle B = \angle E A C $。
$ \because C E \perp A E $，$ \therefore \angle C E A = 90 ^ { \circ } $。
$ \therefore $∠CEA=∠ADB。
在$ \triangle A B D $与$ \triangle C A E $中，$ \left\{ \begin{array} { l } { \angle B = \angle E A C, } \\ { \angle C E A = \angle A D B, } \\ { A B = A C, } \end{array} \right. $
$ \therefore \triangle A B D \cong \triangle C A E $(AAS)。

答案： 证明：$ \because A B = A C $，$ \therefore \angle B = \angle A C B $。
$ \because A D $是$ B C $边上的中线，
$ \therefore A D \perp B C $，即$ \angle A D B = 90 ^ { \circ } $。
$ \because A E // B C $，$ \therefore \angle E A C = \angle A C B $。
$ \therefore \angle B = \angle E A C $。
$ \because C E \perp A E $，$ \therefore \angle C E A = 90 ^ { \circ } $。
$ \therefore \angle C E A = \angle A D B $。
在$ \triangle A B D $与$ \triangle C A E $中，$ \left\{ \begin{array} { l } { \angle B = \angle E A C, } \\ { \angle C E A = \angle A D B, } \\ { A B = A C, } \end{array} \right. $
$ \therefore \triangle A B D \cong \triangle C A E ( A A S ) $。

16. 如图,$AB// FC$,E是DF的中点,若$AB=20,CF=12$,求BD的长度.

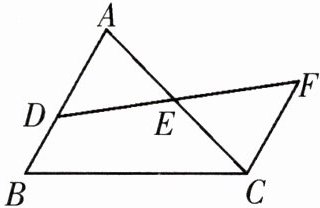
解：$ \because A B // F C $，$ \therefore \angle A D E = \angle E F C $，
$ \because E $是$ D F $的中点，$ \therefore D E = E F $。
在$ \triangle A D E $与$ \triangle C F E $中，$ \left\{ \begin{array} { l } { \angle A D E = \angle E F C, } \\ { D E = E F, } \\ { \angle A E D = \angle C E F, } \end{array} \right. $
$ \therefore \triangle A D E \cong \triangle C F E ( ASA ) $，$ \therefore A D = C F $，
$ \because A B = 20 $，$ C F = 12 $，
$ \therefore A D = 12 $，$ B D = A B - A D = 20 - 12 = 8 $。

答案： 解：$ \because A B // F C $，$ \therefore \angle A D E = \angle E F C $，
$ \because E $是$ D F $的中点，$ \therefore D E = E F $。
在$ \triangle A D E $与$ \triangle C F E $中，$ \left\{ \begin{array} { l } { \angle A D E = \angle E F C, } \\ { D E = E F, } \\ { \angle A E D = \angle C E F, } \end{array} \right. $
$ \therefore \triangle A D E \cong \triangle C F E ( A S A ) $，$ \therefore A D = C F $，
$ \because A B = 20 $，$ C F = 12 $，
$ \therefore A D = 12 $，$ B D = A B - A D = 20 - 12 = 8 $。