2025年文涛书业假期作业快乐暑假七年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年文涛书业假期作业快乐暑假七年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列事件是必然事件的是(
A. 地球绕着太阳转
B. 抛一枚硬币,正面朝上
C. 明天会下雨
D. 打开电视,正在播放新闻
A
)A. 地球绕着太阳转
B. 抛一枚硬币,正面朝上
C. 明天会下雨
D. 打开电视,正在播放新闻
答案:
A
2. 计算$(2a^{2})^{3}\cdot \frac {1}{2}a$正确的结果是(
A. $3a^{7}$
B. $4a^{7}$
C. $a^{7}$
D. $4a^{2}$
B
)A. $3a^{7}$
B. $4a^{7}$
C. $a^{7}$
D. $4a^{2}$
答案:
B
3. 如图,$OA⊥OB$,若$∠1=35^{\circ }$,则$∠2$的度数是(
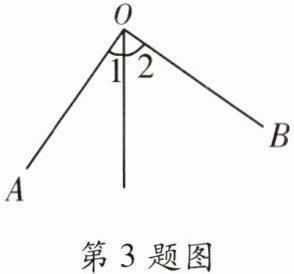
A. $35^{\circ }$
B. $45^{\circ }$
C. $55^{\circ }$
D. $70^{\circ }$
C
) 
A. $35^{\circ }$
B. $45^{\circ }$
C. $55^{\circ }$
D. $70^{\circ }$
答案:
C
4. 将一质地均匀的正方体骰子掷一次,观察向上一面的点数,与点数3相差2的概率是(
A. $\frac {1}{2}$
B. $\frac {1}{3}$
C. $\frac {1}{5}$
D. $\frac {1}{6}$
B
)A. $\frac {1}{2}$
B. $\frac {1}{3}$
C. $\frac {1}{5}$
D. $\frac {1}{6}$
答案:
B
5. 将一副直角三角尺如图放置,若$∠AOD=20^{\circ }$,则$∠BOC$的大小为(

A. $140^{\circ }$
B. $160^{\circ }$
C. $170^{\circ }$
D. $150^{\circ }$
B
)
A. $140^{\circ }$
B. $160^{\circ }$
C. $170^{\circ }$
D. $150^{\circ }$
答案:
B
6. 已知$mn=1,m-n=2$,则$m^{2}n-mn^{2}$的值是(
A. -1
B. 3
C. 2
D. -2
C
)A. -1
B. 3
C. 2
D. -2
答案:
C
7. $M=(a+b)(a-2b),N=-b(a+3b)$,其中$a≠0$,则M、N的大小关系为(
A. $M>N$
B. $M=N$
C. $M<N$
D. 无法确定
A
)A. $M>N$
B. $M=N$
C. $M<N$
D. 无法确定
答案:
A
8. 如图,直线$AC// BD$,AO、BO分别是$∠BAC$、$∠ABD$的平分线,那么$∠BAO$与$∠ABO$之间的大小关系一定为(
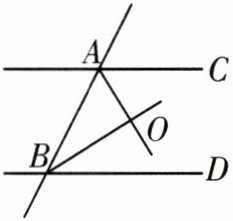
A. 互余
B. 相等
C. 互补
D. 不等
A
)
A. 互余
B. 相等
C. 互补
D. 不等
答案:
A
9. 若$3^{m}=8,3^{n}=2$,则$3^{m+n}$的值为
16
.
答案:
16
10. 如图,直线$l_{1}// l_{2},∠α=∠β,∠1=40^{\circ }$,则$∠2=$

$140^{\circ}$
.
答案:
$140^{\circ}$
11. 若a、b、c为三角形的三边,且a、b满足$\sqrt {a^{2}-9}+(b-2)^{2}=0$,则第三边c的取值范围是
$1 < c < 5$
.
答案:
$1 < c < 5$
12. 如图,点D在$△ABC$边BC的延长线上,CE平分$∠ACD,∠A=80^{\circ },∠B=40^{\circ }$,则$∠ACE$的大小是
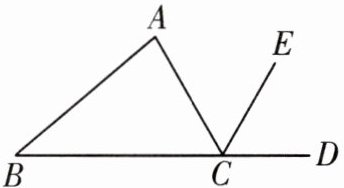
60
度.
答案:
60
13. 如图,在$△ABC$中,$AB=AC,AD⊥BC,CE⊥AB,AE=CE$. 求证:

(1)$△AEF\cong △CEB$;
证明: $\because AD \perp BC, CE \perp AB$,
$\therefore \angle ADC = 90^{\circ}, \angle AEF = \angle CEB = 90^{\circ}$,
$\therefore \angle AFE + \angle EAF = 90^{\circ}, \angle CFD + \angle ECB = 90^{\circ}$,
又 $\because \angle AFE = \angle CFD, \therefore \angle EAF = \angle ECB$.
在 $\triangle AEF$ 和 $\triangle CEB$ 中,
$\angle AEF = \angle CEB, AE = CE, \angle EAF = \angle ECB$,
$\therefore \triangle AEF \cong \triangle CEB$(
(2)$AF=2CD$.
证明: 由 $\triangle AEF \cong \triangle CEB$ 得 $AF =$
在 $\triangle ABC$ 中, $AB = AC, AD \perp BC$,
$\therefore BC = 2CD. \therefore AF = 2CD$.

(1)$△AEF\cong △CEB$;
证明: $\because AD \perp BC, CE \perp AB$,
$\therefore \angle ADC = 90^{\circ}, \angle AEF = \angle CEB = 90^{\circ}$,
$\therefore \angle AFE + \angle EAF = 90^{\circ}, \angle CFD + \angle ECB = 90^{\circ}$,
又 $\because \angle AFE = \angle CFD, \therefore \angle EAF = \angle ECB$.
在 $\triangle AEF$ 和 $\triangle CEB$ 中,
$\angle AEF = \angle CEB, AE = CE, \angle EAF = \angle ECB$,
$\therefore \triangle AEF \cong \triangle CEB$(
ASA
);(2)$AF=2CD$.
证明: 由 $\triangle AEF \cong \triangle CEB$ 得 $AF =$
$BC$
.在 $\triangle ABC$ 中, $AB = AC, AD \perp BC$,
$\therefore BC = 2CD. \therefore AF = 2CD$.
答案:
证明:
(1) $\because AD \perp BC, CE \perp AB$,
$\therefore \angle ADC = 90^{\circ}, \angle AEF = \angle CEB = 90^{\circ}$,
$\therefore \angle AFE + \angle EAF = 90^{\circ}, \angle CFD + \angle ECB = 90^{\circ}$,
又 $\because \angle AFE = \angle CFD, \therefore \angle EAF = \angle ECB$.
在 $\triangle AEF$ 和 $\triangle CEB$ 中,
$\angle AEF = \angle CEB, AE = CE, \angle EAF = \angle ECB$,
$\therefore \triangle AEF \cong \triangle CEB(ASA)$;
(2) 由 $\triangle AEF \cong \triangle CEB$ 得 $AF = BC$.
在 $\triangle ABC$ 中, $AB = AC, AD \perp BC$,
$\therefore BC = 2CD. \therefore AF = 2CD$.
(1) $\because AD \perp BC, CE \perp AB$,
$\therefore \angle ADC = 90^{\circ}, \angle AEF = \angle CEB = 90^{\circ}$,
$\therefore \angle AFE + \angle EAF = 90^{\circ}, \angle CFD + \angle ECB = 90^{\circ}$,
又 $\because \angle AFE = \angle CFD, \therefore \angle EAF = \angle ECB$.
在 $\triangle AEF$ 和 $\triangle CEB$ 中,
$\angle AEF = \angle CEB, AE = CE, \angle EAF = \angle ECB$,
$\therefore \triangle AEF \cong \triangle CEB(ASA)$;
(2) 由 $\triangle AEF \cong \triangle CEB$ 得 $AF = BC$.
在 $\triangle ABC$ 中, $AB = AC, AD \perp BC$,
$\therefore BC = 2CD. \therefore AF = 2CD$.
查看更多完整答案,请扫码查看


