2025年赢在暑假衔接教材五年级数学北师大版合肥工业大学出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年赢在暑假衔接教材五年级数学北师大版合肥工业大学出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
例题
求下面多边形的面积。(单位:cm)
思路分析 这个多边形,我们可以将它分割成几个基本图形。
方法一:
方法二:
方法三:
正确解答 方法一:$20×20+15×15+(15+20)×(40-20-15)÷2= 712.5(cm^{2})$
方法二:$40×15+[20+(40-15)]×(20-15)÷2= 712.5(cm^{2})$
方法三:$40×20-(15+20)×(20-15)÷2= 712.5(cm^{2})$
提优集训五 计算组合图形的面积
概述
组合图形是由两个或两个以上的简单的几何图形组合而成。计算组合图形的面积应看清所求图形是由哪几个基本图形组合而成,或采用平移、旋转、割补、分解、组合等方法将所求图形变成基本图形再计算。



例题
求下面多边形的面积。(单位:cm)
思路分析 这个多边形,我们可以将它分割成几个基本图形。
方法一:
方法二:
方法三:
正确解答 方法一:$20×20+15×15+(15+20)×(40-20-15)÷2= 712.5(cm^{2})$
方法二:$40×15+[20+(40-15)]×(20-15)÷2= 712.5(cm^{2})$
方法三:$40×20-(15+20)×(20-15)÷2= 712.5(cm^{2})$
训练

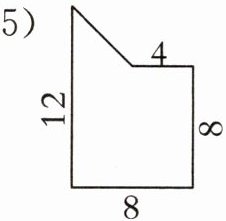

1. 计算下面图形的面积。(单位:cm)
(1)
(2)
(3)
(4)
(5)
(6)

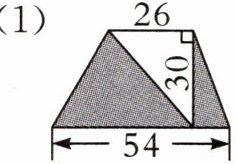
2. 求下面图形中涂色部分的面积。(单位:dm)
(1)
(2)
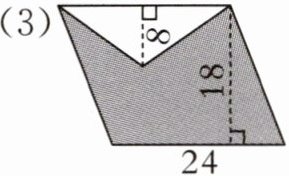
(3)


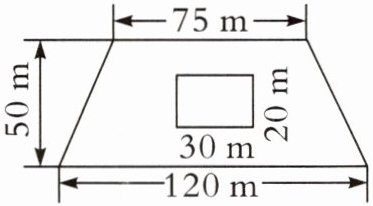

求下面多边形的面积。(单位:cm)
思路分析 这个多边形,我们可以将它分割成几个基本图形。
方法一:
方法二:

方法三:
正确解答 方法一:$20×20+15×15+(15+20)×(40-20-15)÷2= 712.5(cm^{2})$
方法二:$40×15+[20+(40-15)]×(20-15)÷2= 712.5(cm^{2})$
方法三:$40×20-(15+20)×(20-15)÷2= 712.5(cm^{2})$
提优集训五 计算组合图形的面积
概述
组合图形是由两个或两个以上的简单的几何图形组合而成。计算组合图形的面积应看清所求图形是由哪几个基本图形组合而成,或采用平移、旋转、割补、分解、组合等方法将所求图形变成基本图形再计算。



例题
求下面多边形的面积。(单位:cm)
思路分析 这个多边形,我们可以将它分割成几个基本图形。
方法一:
方法二:
方法三:
正确解答 方法一:$20×20+15×15+(15+20)×(40-20-15)÷2= 712.5(cm^{2})$
方法二:$40×15+[20+(40-15)]×(20-15)÷2= 712.5(cm^{2})$
方法三:$40×20-(15+20)×(20-15)÷2= 712.5(cm^{2})$
训练



1. 计算下面图形的面积。(单位:cm)
(1)
(2)

(3)
(4)

(5)
(6)

2. 求下面图形中涂色部分的面积。(单位:dm)
(1)
(2)

(3)





答案:
答案略
1. 计算下面图形的面积。(单位:cm)
(1)
(2)
(3)
(4)
(5)
(6)

提优集训五 计算组合图形的面积
概述
组合图形是由两个或两个以上的简单的几何图形组合而成。计算组合图形的面积应看清所求图形是由哪几个基本图形组合而成,或采用平移、旋转、割补、分解、组合等方法将所求图形变成基本图形再计算。



例题
求下面多边形的面积。(单位:cm)
思路分析 这个多边形,我们可以将它分割成几个基本图形。
方法一:
方法二:
方法三:
正确解答 方法一:$20×20+15×15+(15+20)×(40-20-15)÷2= 712.5(cm^{2})$
方法二:$40×15+[20+(40-15)]×(20-15)÷2= 712.5(cm^{2})$
方法三:$40×20-(15+20)×(20-15)÷2= 712.5(cm^{2})$
训练



1. 计算下面图形的面积。(单位:cm)
(1)
(2)
(3)
(4)
(5)
(6)
2. 求下面图形中涂色部分的面积。(单位:dm)
(1)
(2)
(3)





(1)
(2)

(3)
(4)

(5)
(6)

提优集训五 计算组合图形的面积
概述
组合图形是由两个或两个以上的简单的几何图形组合而成。计算组合图形的面积应看清所求图形是由哪几个基本图形组合而成,或采用平移、旋转、割补、分解、组合等方法将所求图形变成基本图形再计算。



例题
求下面多边形的面积。(单位:cm)
思路分析 这个多边形,我们可以将它分割成几个基本图形。
方法一:
方法二:

方法三:
正确解答 方法一:$20×20+15×15+(15+20)×(40-20-15)÷2= 712.5(cm^{2})$
方法二:$40×15+[20+(40-15)]×(20-15)÷2= 712.5(cm^{2})$
方法三:$40×20-(15+20)×(20-15)÷2= 712.5(cm^{2})$
训练



1. 计算下面图形的面积。(单位:cm)
(1)
(2)
(3)
(4)
(5)
(6)
2. 求下面图形中涂色部分的面积。(单位:dm)
(1)
(2)

(3)





答案:
(1) $50×33 + 35×20÷2 = 1650 + 350 = 2000(cm^{2})$
(2) $10×7 - (10 - 3 - 3 + 6)×3÷2 = 70 - 10×3÷2 = 70 - 15 = 55(cm^{2})$
(3) $70×50÷2 + (40 + 70)×30÷2 = 1750 + 1650 = 3400(cm^{2})$
(4) $(10 + 20)×30÷2 - 10×10÷2 = 450 - 50 = 400(cm^{2})$
(5) $8×8 + (12 - 8)×(8 - 4)÷2 = 64 + 8 = 72(cm^{2})$
(6) $5×5 + 10×(8 - 5) + 7×(8 - 5)÷2 = 25 + 30 + 10.5 = 65.5(cm^{2})$
(1) $50×33 + 35×20÷2 = 1650 + 350 = 2000(cm^{2})$
(2) $10×7 - (10 - 3 - 3 + 6)×3÷2 = 70 - 10×3÷2 = 70 - 15 = 55(cm^{2})$
(3) $70×50÷2 + (40 + 70)×30÷2 = 1750 + 1650 = 3400(cm^{2})$
(4) $(10 + 20)×30÷2 - 10×10÷2 = 450 - 50 = 400(cm^{2})$
(5) $8×8 + (12 - 8)×(8 - 4)÷2 = 64 + 8 = 72(cm^{2})$
(6) $5×5 + 10×(8 - 5) + 7×(8 - 5)÷2 = 25 + 30 + 10.5 = 65.5(cm^{2})$
2. 求下面图形中涂色部分的面积。(单位:dm)
(1)
(2)
提优集训五 计算组合图形的面积
概述
组合图形是由两个或两个以上的简单的几何图形组合而成。计算组合图形的面积应看清所求图形是由哪几个基本图形组合而成,或采用平移、旋转、割补、分解、组合等方法将所求图形变成基本图形再计算。



例题
求下面多边形的面积。(单位:cm)
思路分析 这个多边形,我们可以将它分割成几个基本图形。
方法一:
方法二:
方法三:
正确解答 方法一:$20×20+15×15+(15+20)×(40-20-15)÷2= 712.5(cm^{2})$
方法二:$40×15+[20+(40-15)]×(20-15)÷2= 712.5(cm^{2})$
方法三:$40×20-(15+20)×(20-15)÷2= 712.5(cm^{2})$
训练



1. 计算下面图形的面积。(单位:cm)
(1)
(2)
(3)
(4)
(5)
(6)

2. 求下面图形中涂色部分的面积。(单位:dm)
(1)
(2)
(3)





(4)
(1)
(2)

提优集训五 计算组合图形的面积
概述
组合图形是由两个或两个以上的简单的几何图形组合而成。计算组合图形的面积应看清所求图形是由哪几个基本图形组合而成,或采用平移、旋转、割补、分解、组合等方法将所求图形变成基本图形再计算。



例题
求下面多边形的面积。(单位:cm)
思路分析 这个多边形,我们可以将它分割成几个基本图形。
方法一:
方法二:

方法三:
正确解答 方法一:$20×20+15×15+(15+20)×(40-20-15)÷2= 712.5(cm^{2})$
方法二:$40×15+[20+(40-15)]×(20-15)÷2= 712.5(cm^{2})$
方法三:$40×20-(15+20)×(20-15)÷2= 712.5(cm^{2})$
训练



1. 计算下面图形的面积。(单位:cm)
(1)
(2)

(3)
(4)

(5)
(6)

2. 求下面图形中涂色部分的面积。(单位:dm)
(1)
(2)
(3)





(4)
答案:
(1)
梯形面积:$(26+54)×30÷2=1200(dm^{2})$
空白三角形面积:$26×30÷2=390(dm^{2})$
涂色面积:$1200-390=810(dm^{2})$
(2)
梯形面积:$(8+14)×10÷2=110(dm^{2})$
空白三角形面积:$5×4÷2=10(dm^{2})$
涂色面积:$110-10=100(dm^{2})$
(3)
平行四边形面积:$24×18=432(dm^{2})$
空白三角形面积:$24×8÷2=96(dm^{2})$
涂色面积:$432-96=336(dm^{2})$
(4)
涂色三角形面积:$(5+7)×5÷2=30(dm^{2})$
(1)
梯形面积:$(26+54)×30÷2=1200(dm^{2})$
空白三角形面积:$26×30÷2=390(dm^{2})$
涂色面积:$1200-390=810(dm^{2})$
(2)
梯形面积:$(8+14)×10÷2=110(dm^{2})$
空白三角形面积:$5×4÷2=10(dm^{2})$
涂色面积:$110-10=100(dm^{2})$
(3)
平行四边形面积:$24×18=432(dm^{2})$
空白三角形面积:$24×8÷2=96(dm^{2})$
涂色面积:$432-96=336(dm^{2})$
(4)
涂色三角形面积:$(5+7)×5÷2=30(dm^{2})$
查看更多完整答案,请扫码查看


