2025年赢在暑假衔接教材五年级数学北师大版合肥工业大学出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年赢在暑假衔接教材五年级数学北师大版合肥工业大学出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 盒子里有8颗红色弹珠和2颗黑色弹珠,从中任意摸一个,摸出( )色弹珠的可能性小,摸出( )色弹珠的可能性大。
答案:
解析:本题考查可能性的大小。
数量多的摸出的可能性就大,数量少的摸出的可能性就小。
因为$8>2$,红色弹珠的数量多,黑色弹珠的数量少。
所以摸出黑色弹珠的可能性小,摸出红色弹珠的可能性大。
答案:黑,红。
数量多的摸出的可能性就大,数量少的摸出的可能性就小。
因为$8>2$,红色弹珠的数量多,黑色弹珠的数量少。
所以摸出黑色弹珠的可能性小,摸出红色弹珠的可能性大。
答案:黑,红。
2. 一个不透明的袋子里装有1个白球、3个红球、5个绿球,这些球除颜色外其他均相同。丽丽、亮亮和乐乐从中任意摸一个球决定谁去看电影。摸到白球丽丽去,摸到红球亮亮去,摸到绿球乐乐去。( )去的可能性最大,( )去的可能性最小。
答案:
解析:本题考查的是可能性的大小。
已知袋子里装有1个白球、3个红球、5个绿球。
那么总球数=1+3+5=9(个)。
摸到白球丽丽去,摸到红球亮亮去,摸到绿球乐乐去。
所以摸到白球的可能性=白球数量÷总球数=1÷9=1/9。
摸到红球的可能性=红球数量÷总球数=3÷9=1/3。
摸到绿球的可能性=绿球数量÷总球数=5÷9=5/9。
因为5/9>1/3>1/9,
所以乐乐去的可能性最大,丽丽去的可能性最小。
答案:乐乐;丽丽。
已知袋子里装有1个白球、3个红球、5个绿球。
那么总球数=1+3+5=9(个)。
摸到白球丽丽去,摸到红球亮亮去,摸到绿球乐乐去。
所以摸到白球的可能性=白球数量÷总球数=1÷9=1/9。
摸到红球的可能性=红球数量÷总球数=3÷9=1/3。
摸到绿球的可能性=绿球数量÷总球数=5÷9=5/9。
因为5/9>1/3>1/9,
所以乐乐去的可能性最大,丽丽去的可能性最小。
答案:乐乐;丽丽。
3. 五年级举行庆元旦抽签表演节目活动。

(1)从( )号和( )号箱子里既可能抽出唱歌签,也可能抽出跳舞签。
(2)从( )号箱子里抽到的一定是唱歌签。
(3)从( )号箱子里抽到跳舞签的可能性大些。

(1)从( )号和( )号箱子里既可能抽出唱歌签,也可能抽出跳舞签。
(2)从( )号箱子里抽到的一定是唱歌签。
(3)从( )号箱子里抽到跳舞签的可能性大些。
答案:
解析:本题考查概率的基本概念,可能性的大小与物体数量的多少有关。
(1) 既可能抽出唱歌签,也可能抽出跳舞签的箱子,需要箱子里既有唱歌签又有跳舞签。观察发现 2 号箱子里有 5 个唱歌签和 5 个跳舞签,3 号箱子里有 4 个唱歌签和 6 个跳舞签,都满足条件。
(2) 抽到的一定是唱歌签的箱子,即箱子里全是唱歌签。1 号箱子里有 10 个唱歌签,满足条件。
(3) 抽到跳舞签可能性大的箱子,需要箱子里跳舞签的数量比唱歌签多。3 号箱子里有 6 个跳舞签和 4 个唱歌签,跳舞签数量多于唱歌签,满足条件。
答案:
(1) 2;3
(2) 1
(3) 3
(1) 既可能抽出唱歌签,也可能抽出跳舞签的箱子,需要箱子里既有唱歌签又有跳舞签。观察发现 2 号箱子里有 5 个唱歌签和 5 个跳舞签,3 号箱子里有 4 个唱歌签和 6 个跳舞签,都满足条件。
(2) 抽到的一定是唱歌签的箱子,即箱子里全是唱歌签。1 号箱子里有 10 个唱歌签,满足条件。
(3) 抽到跳舞签可能性大的箱子,需要箱子里跳舞签的数量比唱歌签多。3 号箱子里有 6 个跳舞签和 4 个唱歌签,跳舞签数量多于唱歌签,满足条件。
答案:
(1) 2;3
(2) 1
(3) 3
4. 掷出一个瓶盖后,着地时盖面朝上,甲胜;着地时盖面朝下,乙胜。你认为这个游戏规则( )。(填“公平”或“不公平”)
答案:
解析:要判断这个游戏规则是否公平,需要考虑瓶盖着地时盖面朝上和盖面朝下的可能性是否相等。
由于瓶盖的形状和重量分布,盖面朝上和盖面朝下的概率一般不相等。
通常,瓶盖的形状和重心分布会导致其着地时某一面朝上的概率大于另一面。
因此,这个游戏规则是不公平的。
答案:不公平。
由于瓶盖的形状和重量分布,盖面朝上和盖面朝下的概率一般不相等。
通常,瓶盖的形状和重心分布会导致其着地时某一面朝上的概率大于另一面。
因此,这个游戏规则是不公平的。
答案:不公平。
5. 袋子里现有形状和大小都完全相同的三种球,其中红球和黄球各8个,绿球6个,任意摸一个球,要使摸到绿球的可能性最大,至少还需要放入( )个同样的绿球。
答案:
解析:本题考查的是可能性大小的知识。
要使得摸出绿球的可能性最大,即绿球的数量需要最多。
已知红球和黄球都是8个,绿球6个。
假设放入z个绿球,那么绿球的总数将是 $ (6 + z) $ 个。
为了使绿球的数量最多,需要满足以下条件:
$6 + z > 8$
解这个不等式,我们得到:
$z > 2$
由于z必须是正整数(因为不能放入“部分”球),
所以z的最小值为3。
所以至少需要放入3个绿球,才能使得摸出绿球的可能性最大。
答案:3。
要使得摸出绿球的可能性最大,即绿球的数量需要最多。
已知红球和黄球都是8个,绿球6个。
假设放入z个绿球,那么绿球的总数将是 $ (6 + z) $ 个。
为了使绿球的数量最多,需要满足以下条件:
$6 + z > 8$
解这个不等式,我们得到:
$z > 2$
由于z必须是正整数(因为不能放入“部分”球),
所以z的最小值为3。
所以至少需要放入3个绿球,才能使得摸出绿球的可能性最大。
答案:3。
1. 要使指针停在阴影区域的可能性最大,应选( )圆盘。


答案:
解析:本题考查了可能性的大小,哪种颜色区域面积越大,指针指向该区域的可能性就越大。
A 圆盘中阴影区域有 4 份,空白区域有 4 份;
B 圆盘中阴影区域有 3 份,空白区域有 5 份;
C 圆盘中阴影区域有 5 份,空白区域有 3 份。
C 圆盘中阴影区域份数最多,所以指针停在阴影区域的可能性最大。
答案:C。
A 圆盘中阴影区域有 4 份,空白区域有 4 份;
B 圆盘中阴影区域有 3 份,空白区域有 5 份;
C 圆盘中阴影区域有 5 份,空白区域有 3 份。
C 圆盘中阴影区域份数最多,所以指针停在阴影区域的可能性最大。
答案:C。
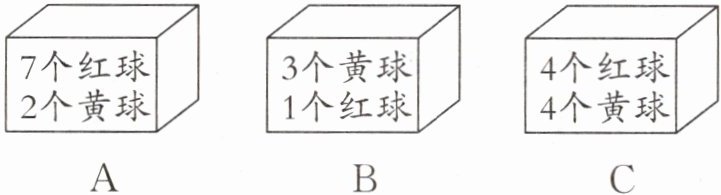
2. 小明和小伙伴玩摸球游戏,要使游戏公平,应选用( )号盒子的球。

答案:
解析:本题考查游戏公平性的判断,关键在于比较每个盒子中摸到不同颜色球的可能性是否相等。
选项A中,红球有7个,黄球有2个,红球数量远多于黄球,摸到红球的可能性大,游戏不公平。
选项B中,黄球有3个,红球有1个,黄球数量多于红球,摸到黄球的可能性大,游戏不公平。
选项C中,红球有4个,黄球有4个,红球和黄球数量相等,摸到红球和黄球的可能性相同,游戏公平。
答案:C。
选项A中,红球有7个,黄球有2个,红球数量远多于黄球,摸到红球的可能性大,游戏不公平。
选项B中,黄球有3个,红球有1个,黄球数量多于红球,摸到黄球的可能性大,游戏不公平。
选项C中,红球有4个,黄球有4个,红球和黄球数量相等,摸到红球和黄球的可能性相同,游戏公平。
答案:C。
3. 盒子里有两种颜色的球(除颜色外,其他完全相同),小奇摸了50次,摸球情况如下表。根据表中数据推测,错误的是( )。
| | 红球 | 黄球 |
| 次数 | 9 | 41 |
A.盒子里黄球可能多
B.如果小奇再摸一次,摸到的可能是黄球
C.如果小奇再摸一次,摸到的一定是黄球
| | 红球 | 黄球 |
| 次数 | 9 | 41 |

A.盒子里黄球可能多
B.如果小奇再摸一次,摸到的可能是黄球
C.如果小奇再摸一次,摸到的一定是黄球
答案:
解析:本题考查根据摸球实验数据推测盒子中球的情况以及可能性的知识。
选项A:在大量重复试验中,某一事件发生的频率近似等于这一事件发生的概率。小奇摸了50次,摸到黄球41次,摸到红球9次,摸到黄球的次数远多于红球,说明摸到黄球的可能性较大,由此可以推测盒子里黄球可能多,该选项正确。
选项B:因为盒子里有红球和黄球两种球,所以每次摸球时,都有摸到红球或黄球的可能性,如果小奇再摸一次,摸到的可能是黄球,该选项正确。
选项C:虽然摸到黄球的可能性较大,但可能性并不等同于确定性,即使再摸一次,也有可能摸到红球,并不是一定摸到黄球,该选项错误。
答案:C。
选项A:在大量重复试验中,某一事件发生的频率近似等于这一事件发生的概率。小奇摸了50次,摸到黄球41次,摸到红球9次,摸到黄球的次数远多于红球,说明摸到黄球的可能性较大,由此可以推测盒子里黄球可能多,该选项正确。
选项B:因为盒子里有红球和黄球两种球,所以每次摸球时,都有摸到红球或黄球的可能性,如果小奇再摸一次,摸到的可能是黄球,该选项正确。
选项C:虽然摸到黄球的可能性较大,但可能性并不等同于确定性,即使再摸一次,也有可能摸到红球,并不是一定摸到黄球,该选项错误。
答案:C。
三、动手操作。(26分)
1. 小丽和小华做摸球游戏,每次在口袋里任意摸出一个球,摸到黑球小丽赢,摸到白球小华赢。用下面哪些口袋做摸球游戏是公平的?哪些是不公平的?连一连。(12分)
公平 不公平

2. 涂一涂,画一画。(14分)
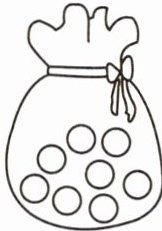
(1)给小球涂上颜色,使任意摸一个球,摸到红球的可能性最大。
(2)给转盘分一分、涂一涂,使转到红色、黄色、蓝色区域的可能性相等。
1. 小丽和小华做摸球游戏,每次在口袋里任意摸出一个球,摸到黑球小丽赢,摸到白球小华赢。用下面哪些口袋做摸球游戏是公平的?哪些是不公平的?连一连。(12分)
公平 不公平

2. 涂一涂,画一画。(14分)
(1)给小球涂上颜色,使任意摸一个球,摸到红球的可能性最大。

(2)给转盘分一分、涂一涂,使转到红色、黄色、蓝色区域的可能性相等。

答案:
1. 第一个口袋(3黑2白)——不公平;第二个口袋(2黑2白)——公平;第三个口袋(2黑3白)——不公平;第四个口袋(4黑2白)——不公平。
2.
(1) 涂7个红球,其他颜色球的数量少于7个(具体涂法略,需实际涂色)。
(2) 将转盘平均分成3份,分别涂红色、黄色、蓝色(具体分法和涂法略,需实际画图涂色)。
2.
(1) 涂7个红球,其他颜色球的数量少于7个(具体涂法略,需实际涂色)。
(2) 将转盘平均分成3份,分别涂红色、黄色、蓝色(具体分法和涂法略,需实际画图涂色)。
查看更多完整答案,请扫码查看


