第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页

答案:
底×高;(上底 + 下底)×高÷2
例1 你能想办法求出下面梯形的面积吗?(每个小方格表示1平方厘米)
你想怎样做?与同学交流。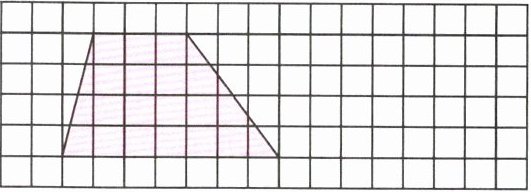
过程探索 例题图中的梯形可以分成1个长方形和2个三角形,也可以分成1个平行四边形和1个三角形,还可以补一个完全一样的梯形拼成一个()。这样用1个长方形+2个三角形或1个平行四边形+1个三角形或平行四边形的面积÷2,都可以求出这个梯形的面积。图中每个小方格表示1平方厘米,运用以前学过的知识,可以采用不同的方法求出梯形的面积。
完全解答 方法一:数方格法,不满一格的按半格来计算。梯形共有15个整格,10个半格,所以面积是20平方厘米。
方法二:转化法。可以把梯形分成1个长方形和2个三角形或把梯形分成1个平行四边形和1个三角形;也可以再补一个完全一样的梯形,拼成一个平行四边形后,用平行四边形的面积除以2。所以梯形的面积是20平方厘米。
你想怎样做?与同学交流。

过程探索 例题图中的梯形可以分成1个长方形和2个三角形,也可以分成1个平行四边形和1个三角形,还可以补一个完全一样的梯形拼成一个()。这样用1个长方形+2个三角形或1个平行四边形+1个三角形或平行四边形的面积÷2,都可以求出这个梯形的面积。图中每个小方格表示1平方厘米,运用以前学过的知识,可以采用不同的方法求出梯形的面积。
完全解答 方法一:数方格法,不满一格的按半格来计算。梯形共有15个整格,10个半格,所以面积是20平方厘米。
方法二:转化法。可以把梯形分成1个长方形和2个三角形或把梯形分成1个平行四边形和1个三角形;也可以再补一个完全一样的梯形,拼成一个平行四边形后,用平行四边形的面积除以2。所以梯形的面积是20平方厘米。
答案:
平行四边形
例2 从教材第117页选两个梯形剪下来,把它们拼成平行四边形,求出拼成的平行四边形和每个梯形的面积,再通过交流完成下表。
|拼成的平行四边形| | |梯形| | | |
|底/cm|高/cm|面积/cm^2|上底/cm|下底/cm|高/cm|面积/cm^2|
| | | | | | | |
小组讨论:
(1)拼成平行四边形的两个梯形有什么关系?
(2)拼成的平行四边形的底与梯形的上底、下底有什么关系?平行四边形的高与梯形的高有什么关系?每个梯形的面积与拼成的平行四边形的面积呢?
(3)根据平行四边形的面积公式,怎样求梯形的面积?
梯形的面积= (上底+下底)×高÷2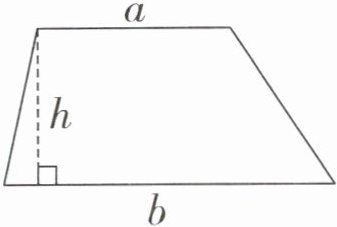
如果用S表示梯形的面积,用a、b和h分别表示梯形的上底、下底和高,上面的公式可以写成:$S= (a+b)×h÷2$。
过程探索 拼成平行四边形要找两个形状、大小完全相同的梯形,拼组的过程如下:

因为平行四边形的面积= (),拼成的平行四边形的底等于梯形的上底与下底的和,拼成的平行四边形的高等于梯形的高,所以梯形的面积= ()。
完全解答
|拼成的行四边形| | |梯形| | | |
|底/cm|高/cm|面积/cm^2|上底/cm|下底/cm|高/cm|面积/cm^2|
|22|3|66|8|14|3|33|
|9|4|36|3|6|4|18|
|12|5|60|4|8|5|30|
通过观察上表可知:(1)拼成平行四边形的两个梯形完全一样。(2)拼成的平行四边形的底等于梯形的上底与下底的和,拼成的平行四边形的高等于梯形的高,每个梯形的面积等于拼成的平行四边形面积的一半。(3)梯形的面积= (上底+下底)×高÷2。
|拼成的平行四边形| | |梯形| | | |
|底/cm|高/cm|面积/cm^2|上底/cm|下底/cm|高/cm|面积/cm^2|
| | | | | | | |
小组讨论:
(1)拼成平行四边形的两个梯形有什么关系?
(2)拼成的平行四边形的底与梯形的上底、下底有什么关系?平行四边形的高与梯形的高有什么关系?每个梯形的面积与拼成的平行四边形的面积呢?
(3)根据平行四边形的面积公式,怎样求梯形的面积?
梯形的面积= (上底+下底)×高÷2

如果用S表示梯形的面积,用a、b和h分别表示梯形的上底、下底和高,上面的公式可以写成:$S= (a+b)×h÷2$。
过程探索 拼成平行四边形要找两个形状、大小完全相同的梯形,拼组的过程如下:

因为平行四边形的面积= (),拼成的平行四边形的底等于梯形的上底与下底的和,拼成的平行四边形的高等于梯形的高,所以梯形的面积= ()。
完全解答
|拼成的行四边形| | |梯形| | | |
|底/cm|高/cm|面积/cm^2|上底/cm|下底/cm|高/cm|面积/cm^2|
|22|3|66|8|14|3|33|
|9|4|36|3|6|4|18|
|12|5|60|4|8|5|30|
通过观察上表可知:(1)拼成平行四边形的两个梯形完全一样。(2)拼成的平行四边形的底等于梯形的上底与下底的和,拼成的平行四边形的高等于梯形的高,每个梯形的面积等于拼成的平行四边形面积的一半。(3)梯形的面积= (上底+下底)×高÷2。
答案:
底×高 (上底+下底)×高÷2
查看更多完整答案,请扫码查看


