第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
3. 如果直角梯形的一个内角是$75^{\circ}$(如图),那么这个直角梯形中$∠1$是多少度?
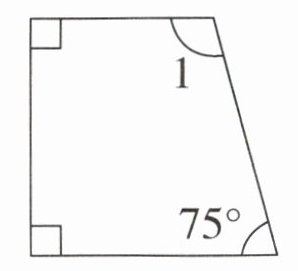

答案:
$360^{\circ}-90^{\circ} × 2-75^{\circ}=105^{\circ}$
4. 看图计算。
(1)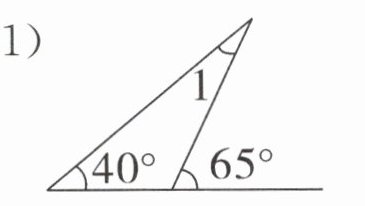
$∠1 = $()$^{\circ}$。
(2)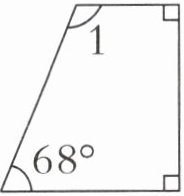
上图是直角梯形,$∠1 = $()$^{\circ}$。
(3)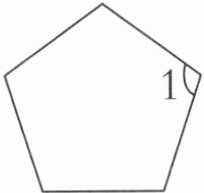
上图是正五边形,$∠1 = $()$^{\circ}$。
(1)

$∠1 = $()$^{\circ}$。
(2)

上图是直角梯形,$∠1 = $()$^{\circ}$。
(3)

上图是正五边形,$∠1 = $()$^{\circ}$。
答案:
(1)25
(2)112
(3)108
(1)25
(2)112
(3)108
5. 在四边形ABCD中,$∠A = 120^{\circ}$,若$∠A的度数是∠B$的3倍,是$∠C$的4倍,则$∠D$是多少度?
答案:
$\angle B=120^{\circ} ÷ 3=40^{\circ} \quad \angle C=120^{\circ} ÷ 4=30^{\circ}$
$\angle D=360^{\circ}-120^{\circ}-40^{\circ}-30^{\circ}=170^{\circ}$
提示 $\angle A=3 \angle B=4 \angle C$, 据此可以先分别求出 $\angle B$ 和 $\angle C$ 的度数, 再用 $360^{\circ}$ 分别减去三个角的度数, 从而求出 $\angle D$ 的度数。
$\angle D=360^{\circ}-120^{\circ}-40^{\circ}-30^{\circ}=170^{\circ}$
提示 $\angle A=3 \angle B=4 \angle C$, 据此可以先分别求出 $\angle B$ 和 $\angle C$ 的度数, 再用 $360^{\circ}$ 分别减去三个角的度数, 从而求出 $\angle D$ 的度数。
6. 一张正方形桌面,不小心用刀砍去了一个角,请画出该桌子被砍去角之后的桌面形状,并求出对应桌面平面图形的内角和。
答案:


7. 明明在计算一个多边形的内角和时,少数了一条边,结果得出的内角和是$1080^{\circ}$,这个多边形应该是几边形?它的内角和应该是多少?
答案:
九边形, 内角和为 $1260^{\circ}$ 。
提示 这个多边形一共有 $\left(1080^{\circ}+180^{\circ}\right) ÷$ $180^{\circ}+2=9$ (条) 边, 内角和是 $(9-2) × 180^{\circ}=$ $1260^{\circ}$ 。
提示 这个多边形一共有 $\left(1080^{\circ}+180^{\circ}\right) ÷$ $180^{\circ}+2=9$ (条) 边, 内角和是 $(9-2) × 180^{\circ}=$ $1260^{\circ}$ 。
查看更多完整答案,请扫码查看


