《2025年暑假集训五年级数学人教版合肥工业大学出版社》

1.(1)从正面看,(②)与(⑥)的形状相同,(④)与(⑤)的形状相同。
(2)从左面看是的有(②③)。
(3)从(上)面看,它们的形状各不相同。

答案： 1.
(1)②　⑥　④　⑤　
(2)②③　
(3)上

2.(1)图形B可以看成由图形A绕点(Q)按顺时针方向旋转 $90^{\circ}$,又向(下)平移(2)格得到的。
(2)图形C可以看成由图形B绕点(O)按顺时针方向旋转(90°),又向(左)平移(2)格得到的。
(3)图形D可以看成由图形(C)绕点(I)按(顺时针)方向旋转(90°),又向(上)平移(2)格得到的。(或图形D可以看成由图形(A)绕点(P)按(逆时针)方向旋转(90°),又向(下)平移(2)格得到的。)

答案： 2.
(1)Q　下　2　
(2)O　90°　左　2　
(3)C　I　顺时针　90°　上　2(或A　P 逆时针　90°　下　2)

1.从左面观察,形状是(A)。

答案： A

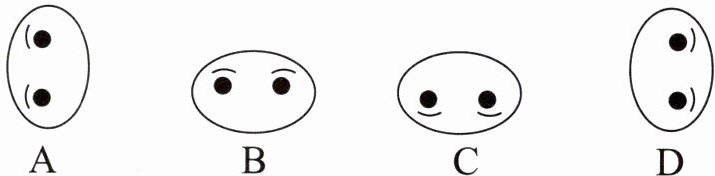
2.如下图,图C是由图(B)顺时针旋转 $180^{\circ}$ 得到的。

答案： B

3.图A(D)可以成为图B。

A.顺时针旋转 $90^{\circ}$
B.逆时针旋转 $90^{\circ}$
C.平移
D.顺时针旋转 $180^{\circ}$

答案： D

4.如图,图形旋转一定角度后,能与自身重合,则旋转的角度可能是(C)。

A.$30^{\circ}$
B.$60^{\circ}$
C.$90^{\circ}$
D.$120^{\circ}$

答案： C

5.在下面的运动中,(D)既属于平移又属于旋转。
A.时针和分针的运动
B.小木块从高处自由落下
C.工作中的电风扇
D.行进中的自行车的车轮

答案： D

1.将图中的小旗子和“N”字母分别绕O点、 $O'$ 点顺时针旋转 $90^{\circ}$。(6分)

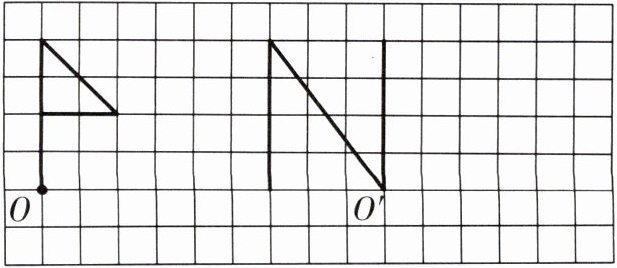
答案： 本题可根据旋转的性质，通过确定图形关键点旋转后的位置，进而画出旋转后的图形。
步骤一：明确旋转的性质
在平面内，将一个图形绕一点按某个方向转动一个角度，这样的运动叫做图形的旋转。这个定点叫做旋转中心，转动的角度叫做旋转角。旋转的性质为：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等。
步骤二：确定小旗子绕$O$点顺时针旋转$90^{\circ}$后的图形
先确定小旗子的关键点（如三角形的三个顶点和旗杆的端点）。
对于每个关键点，根据旋转性质，绕$O$点顺时针旋转$90^{\circ}$。例如，设小旗子上某一关键点$A$，连接$OA$，以$O$为顶点，$OA$为一边，顺时针作$90^{\circ}$角，在角的另一边截取$OA^\prime = OA$，得到$A$点旋转后的对应点$A^\prime$。
用同样的方法确定小旗子其他关键点旋转后的位置，然后依次连接这些对应点，得到小旗子绕$O$点顺时针旋转$90^{\circ}$后的图形。
步骤三：确定“$N$”字母绕$O'$点顺时针旋转$90^{\circ}$后的图形
找出“$N$”字母的关键点（如线段的端点）。
对每个关键点，绕$O'$点顺时针旋转$90^{\circ}$。设“$N$”字母上一关键点$B$，连接$O'B$，以$O'$为顶点，$O'B$为一边，顺时针作$90^{\circ}$角，在角的另一边截取$O'B^\prime = O'B$，得到$B$点旋转后的对应点$B^\prime$。
确定“$N$”字母其他关键点旋转后的位置，依次连接这些对应点，得到“$N$”字母绕$O'$点顺时针旋转$90^{\circ}$后的图形。
综上，按照上述方法可画出小旗子绕$O$点、“$N$”字母绕$O'$点顺时针旋转$90^{\circ}$后的图形（由于无法直接绘制图形，你可根据上述步骤自行完成作图）。