2025年暑假集训五年级数学人教版合肥工业大学出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假集训五年级数学人教版合肥工业大学出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. $ 6400mL = $
6.4
$L $ $ 7.8m^{3} = $7800
$dm^{3} $$ 5.6m^{3} = $5600
$L $ $ 9000cm^{3} = $0.009
$m^{3} $
答案:
解析:本题考查单位换算知识点,需要用到体积、容积单位间的进率及换算方法,对于$1L = 1000mL$,$1m^{3}=1000dm^{3}$,$1dm^{3}=1L$,$1m^{3}=1000000cm^{3}$这些换算关系要熟练掌握。
答案:
$ 6400mL = (6.4)L $
$ 7.8m^{3} = (7800)dm^{3} $
$ 5.6m^{3} = (5600)L $
$ 9000cm^{3} = (0.009)m^{3} $
答案:
$ 6400mL = (6.4)L $
$ 7.8m^{3} = (7800)dm^{3} $
$ 5.6m^{3} = (5600)L $
$ 9000cm^{3} = (0.009)m^{3} $
2. 一个正方体的表面积是 $ 24dm^{2} $,它的每个面的面积是 $ (\quad)dm^{2} $,棱长是 $ (\quad)dm $,体积是 $ (\quad)dm^{3} $。
(
(
(
(
4
)(
2
)(
8
)
答案:
解析:
首先,正方体的一个面的面积是总表面积除以6(因为正方体有6个面,且每个面的面积相同)。
然后,利用正方形的面积公式$s = a^{2}$(s是面积,a是边长),可以求出正方体的棱长a。
最后,利用正方体的体积公式$V = a^{3}$(V是体积,a是边长)来求出正方体的体积。
每个面的面积计算:
正方体有6个面,每个面的面积为:
$24 ÷ 6 = 4(dm^{2})$。
棱长的计算:
因为每个面是正方形,且面积为4平方分米,所以棱长a满足:
$a^{2} = 4$。
解得:$a = 2(dm)$(负值舍去,因为边长不能为负)。
体积的计算:
正方体的体积为:
$V = a^{3} = 2^{3} = 8(dm^{3})$。
答案:
每个面的面积是 $4dm^{2}$,棱长是 $2dm$,体积是 $8dm^{3}$。
首先,正方体的一个面的面积是总表面积除以6(因为正方体有6个面,且每个面的面积相同)。
然后,利用正方形的面积公式$s = a^{2}$(s是面积,a是边长),可以求出正方体的棱长a。
最后,利用正方体的体积公式$V = a^{3}$(V是体积,a是边长)来求出正方体的体积。
每个面的面积计算:
正方体有6个面,每个面的面积为:
$24 ÷ 6 = 4(dm^{2})$。
棱长的计算:
因为每个面是正方形,且面积为4平方分米,所以棱长a满足:
$a^{2} = 4$。
解得:$a = 2(dm)$(负值舍去,因为边长不能为负)。
体积的计算:
正方体的体积为:
$V = a^{3} = 2^{3} = 8(dm^{3})$。
答案:
每个面的面积是 $4dm^{2}$,棱长是 $2dm$,体积是 $8dm^{3}$。
3. 长方体的长、宽、高分别扩大到原来的 2 倍,它的表面积扩大到原来的 $(\quad
4
\quad)$ 倍,体积扩大到原来的 $(\quad8
\quad)$ 倍。
答案:
解析:本题主要考查长方体的表面积和体积公式,以及如何通过计算得出表面积和体积扩大的倍数。
设原来的长方体的长、宽、高分别为$a$,$b$,$c$。
则原表面积$S_{原}=2(ab+ac+bc)$,原体积$V_{原}=abc$。
当长、宽、高分别扩大到原来的2倍时,新的长、宽、高分别为$2a$,$2b$,$2c$。
新表面积$S_{新}=2(2a × 2b+2a × 2c+2b × 2c)=4 × 2(ab+ac+bc)=4S_{原}$,
新体积$V_{新}=2a × 2b × 2c=8abc=8V_{原}$。
因此,表面积扩大到原来的4倍,体积扩大到原来的8倍。
答案:4;8。
设原来的长方体的长、宽、高分别为$a$,$b$,$c$。
则原表面积$S_{原}=2(ab+ac+bc)$,原体积$V_{原}=abc$。
当长、宽、高分别扩大到原来的2倍时,新的长、宽、高分别为$2a$,$2b$,$2c$。
新表面积$S_{新}=2(2a × 2b+2a × 2c+2b × 2c)=4 × 2(ab+ac+bc)=4S_{原}$,
新体积$V_{新}=2a × 2b × 2c=8abc=8V_{原}$。
因此,表面积扩大到原来的4倍,体积扩大到原来的8倍。
答案:4;8。
4. 用 3 个棱长是 3cm 的小正方体拼成一个长方体,表面积减少 $(\quad)cm^{2} $,体积 $(\quad) $。
36
81cm³
答案:
解析:
本题考查的知识点是长方体和正方体的表面积和体积计算,以及拼接后表面积的变化。
首先,一个小正方体的棱长是3cm,所以一个小正方体的表面积是$6 × (3× 3) = 54({cm}^{2})$(因为正方体有6个面,每个面的面积是$3× 3=9({cm}^{2})$)。
三个小正方体的总表面积是$3 × 54 = 162({cm}^{2})$。
当我们将三个小正方体拼接成一个长方体时,它们会共享一些面。
具体来说,每两个相邻的小正方体会共享两个面,所以拼接后的长方体表面积会减少。
三个小正方体拼接成一条直线形状的长方体,会减少4个面(因为两个相邻的小正方体共享两个面,三个小正方体就有两对相邻面,即4个共享面)。
所以,拼接后的长方体表面积是$162 - 4 × 9 = 162 - 36 = 126({cm}^{2})$。
但题目问的是表面积减少了多少,所以答案是$162 - 126 = 36({cm}^{2})$,
因为减少了4个面,每个面$9 ({cm}^{2})$,也可以直接写成$4 × 9 = 36({cm}^{2})$。
接下来,计算体积。
一个小正方体的体积是$3× 3× 3= 27({cm}^{3})$。
所以,三个小正方体的总体积是$3 × 27 = 81({cm}^{3})$。
拼接后的长方体体积与三个小正方体的总体积相同,因为物质是守恒的,没有增加也没有减少。
所以,拼接后的长方体体积也是$81({cm}^{3})$。
答案:
表面积减少 $36{cm}^{2}$;体积 $81{cm}^{3}$。
本题考查的知识点是长方体和正方体的表面积和体积计算,以及拼接后表面积的变化。
首先,一个小正方体的棱长是3cm,所以一个小正方体的表面积是$6 × (3× 3) = 54({cm}^{2})$(因为正方体有6个面,每个面的面积是$3× 3=9({cm}^{2})$)。
三个小正方体的总表面积是$3 × 54 = 162({cm}^{2})$。
当我们将三个小正方体拼接成一个长方体时,它们会共享一些面。
具体来说,每两个相邻的小正方体会共享两个面,所以拼接后的长方体表面积会减少。
三个小正方体拼接成一条直线形状的长方体,会减少4个面(因为两个相邻的小正方体共享两个面,三个小正方体就有两对相邻面,即4个共享面)。
所以,拼接后的长方体表面积是$162 - 4 × 9 = 162 - 36 = 126({cm}^{2})$。
但题目问的是表面积减少了多少,所以答案是$162 - 126 = 36({cm}^{2})$,
因为减少了4个面,每个面$9 ({cm}^{2})$,也可以直接写成$4 × 9 = 36({cm}^{2})$。
接下来,计算体积。
一个小正方体的体积是$3× 3× 3= 27({cm}^{3})$。
所以,三个小正方体的总体积是$3 × 27 = 81({cm}^{3})$。
拼接后的长方体体积与三个小正方体的总体积相同,因为物质是守恒的,没有增加也没有减少。
所以,拼接后的长方体体积也是$81({cm}^{3})$。
答案:
表面积减少 $36{cm}^{2}$;体积 $81{cm}^{3}$。
5. 一个长 8cm、宽 6cm、高 3cm 的长方体,最多能分割成 $(\quad)$ 个长 4cm、宽 3cm、高 1cm 的长方体。
12
答案:
解析:本题考查长方体体积的计算及切割拼凑问题。需要分别计算大长方体和小长方体的体积,通过体积的比值来确定最多能分割的个数。
大长方体体积$V_1 = 8×6×3 = 144$(立方厘米),
小长方体体积$V_2 = 4×3×1 = 12$(立方厘米),
则可分割的个数$n=\frac{V_1}{V_2}=\frac{144}{12}=12$(个)。
答案:12
大长方体体积$V_1 = 8×6×3 = 144$(立方厘米),
小长方体体积$V_2 = 4×3×1 = 12$(立方厘米),
则可分割的个数$n=\frac{V_1}{V_2}=\frac{144}{12}=12$(个)。
答案:12
二、判断。(对的打“√”,错的打“×”)(5 分)
1. 一个长方体(非正方体)中,最多有 8 条棱的长度相等。(
2. 体积相等的长方体,表面积也一定相等。(
3. 体积单位之间的进率是 1000。(
4. 一台冰箱的容积是 196 升,它的体积就是 196 立方分米。(
5. 用 12 个 $ 1cm^{3} $ 的正方体拼成的每一个立体图形,它们的体积都是 $ 12cm^{3} $。(
1. 一个长方体(非正方体)中,最多有 8 条棱的长度相等。(
√
)2. 体积相等的长方体,表面积也一定相等。(
×
)3. 体积单位之间的进率是 1000。(
×
)4. 一台冰箱的容积是 196 升,它的体积就是 196 立方分米。(
×
)5. 用 12 个 $ 1cm^{3} $ 的正方体拼成的每一个立体图形,它们的体积都是 $ 12cm^{3} $。(
√
)
答案:
1. √
2. ×
3. ×
4. ×
5. √
2. ×
3. ×
4. ×
5. √
1. 长方体的高一定,底面积越大,体积(
A.越大
B.不变
C.越小
A
)。A.越大
B.不变
C.越小
答案:
A。
2. $ a^{3} $ 表示(
A.$ a×3 $
B.$ a·a·a $
C.$ a + 3 $
B
)。A.$ a×3 $
B.$ a·a·a $
C.$ a + 3 $
答案:
B。
3. 把这张硬纸片对折起来拼成一个正方体,和 3 号面相对的面是( )号面,和 1 号面相对的面是( )号面。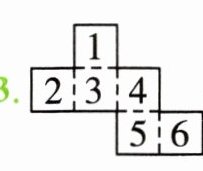
A.4
B.5
C.6

A.4
B.5
C.6
答案:
答案略
4. 长方体的长扩大到原来的 5 倍,宽缩小到原来的 $ \frac{1}{5} $,高不变,体积(
A.扩大到原来的 5 倍
B.缩小到原来的 $ \frac{1}{5} $
C.不变
C
)。A.扩大到原来的 5 倍
B.缩小到原来的 $ \frac{1}{5} $
C.不变
答案:
C。
5. 如图所示,在一个棱长为 2 分米的正方体的一角挖掉一块棱长为 1 分米的小正方体,则剩余图形的表面积(

A.与原来相等
B.比原来大
C.比原来小
D.不能确定
A
)。
A.与原来相等
B.比原来大
C.比原来小
D.不能确定
答案:
A。
|图形|长|宽|高|棱长总和|体积|
|长方体|4.2m|2m|1.5m|
|长方体|4.8cm|3cm|
|长方体|
|正方体|棱长是 12cm| - | - |
|长方体|4.2m|2m|1.5m|
30.8m
|12.6m³
||长方体|4.8cm|3cm|
5cm
|51.2cm
|72cm³||长方体|
8dm
|2dm|5dm|60dm|80dm³
||正方体|棱长是 12cm| - | - |
144cm
|1728cm³
|
答案:
|图形|长|宽|高|棱长总和|体积|
| ---- | ---- | ---- | ---- | ---- | ---- |
|长方体|$4.2m$|$2m$|$1.5m$|$30.8m$|$12.6m^{3}$|
|长方体|$4.8cm$|$3cm$|$5cm$|$51.2cm$|$72cm^{3}$|
|长方体|$8dm$|$2dm$|$5dm$|$60dm$|$80dm^{3}$|
|正方体|棱长是 $12cm$| - | - |$144cm$|$1728cm^{3}$|
|图形|长|宽|高|棱长总和|体积|
| ---- | ---- | ---- | ---- | ---- | ---- |
|长方体|$4.2m$|$2m$|$1.5m$|$30.8m$|$12.6m^{3}$|
|长方体|$4.8cm$|$3cm$|$5cm$|$51.2cm$|$72cm^{3}$|
|长方体|$8dm$|$2dm$|$5dm$|$60dm$|$80dm^{3}$|
|正方体|棱长是 $12cm$| - | - |$144cm$|$1728cm^{3}$|
五、计算下面图形的表面积和体积。(单位:cm)(12 分)
1.

2.

1.

2.

答案:
1.1.表面积:6×6×6=216(cm²) 体积:6×6×6= 216(cm³)
2.表面积:18×8×2+8×7×2+18×7×2=652(cm²) 体积:18×8×7=1008(cm³)
2.表面积:18×8×2+8×7×2+18×7×2=652(cm²) 体积:18×8×7=1008(cm³)
查看更多完整答案,请扫码查看


