《2025年暑假集训五年级数学人教版合肥工业大学出版社》

例3 下图中阴影部分的面积是$15cm^{2}$，三角形$ABC$的面积是多少平方厘米？

答案： 本题可先根据三角形面积公式求出三角形$ABC$的高，再根据三角形面积公式求出其面积。
三角形面积公式为$S = \frac{1}{2}ah$（其中$S$表示面积，$a$表示底边长，$h$表示这条底边对应的高）。
已知阴影部分（小三角形）的面积是$15cm^2$，底为$3cm$，将数值代入上述公式可得：
$15=\frac{1}{2}×3× h$
$h = 15×2÷3$
$h = 10$（$cm$）
即三角形$ABC$以$BC$为底边时的高为$10cm$。
三角形$ABC$的底$BC = 3 + 5 = 8$（$cm$），高为$10cm$，将其代入三角形面积公式可得：
$S_{ABC}=\frac{1}{2}×8×10$
$S_{ABC}=40$（$cm^2$）
答：三角形$ABC$的面积是$40$平方厘米。

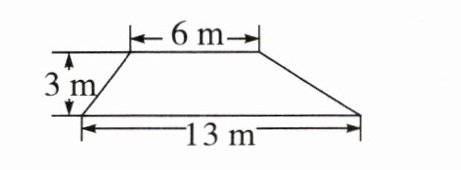
例4 某大坝的横截面的一部分是梯形(如下图)，求它的面积。

答案： 解析：本题可根据梯形的面积公式来求解该梯形的面积，梯形的面积公式为$S=(a + b)h÷2$（其中$S$表示梯形面积，$a$表示梯形的上底，$b$表示梯形的下底，$h$表示梯形的高）。
从图中可知梯形的上底$a = 6m$，下底$b = 13m$，高$h = 3m$，将这些数据代入梯形面积公式进行计算。
答案：
$S=(a + b)h÷2$
$=(6 + 13)×3÷2$
$=19×3÷2$
$=57÷2$
$= 28.5$（$m^{2}$）
答：它的面积是$28.5m^{2}$。

例5 下图是由边长分别为$6cm$,$10cm$,$8cm$的三个正方形组成的组合图形,求阴影部分的面积。

三角形$ABC$的面积：$ (10 + 8) × 10 ÷ 2 = 90(cm^{2}) $
下面空白三角形的面积：$ (6 + 10 + 8) × 6 ÷ 2 = 72(cm^{2}) $
阴影部分的面积：$ 36 + 90 - 72 = 54(cm^{2}) $

答案： 解析：本题可通过用两个正方形的面积之和减去空白三角形的面积来求阴影部分的面积，也可分别求出相关三角形的面积，再通过面积关系求出阴影部分面积。
答案：
方法一：
正方形面积分别为：
$S_1=6×6 = 36(cm^2)$，
$S_2=10×10 = 100(cm^2)$，
$S_3=8×8 = 64(cm^2)$。
$\triangle ABC$的面积：
$S_{\triangle ABC}=(10 + 8)×10÷2 = 90(cm^2)$。
下面空白三角形的面积：
$S_{空白}=(6 + 10 + 8)×6÷2 = 72(cm^2)$。
阴影部分的面积：
$S = S_1+S_{\triangle ABC}-S_{空白}=36 + 90 - 72 = 54(cm^2)$。
方法二：
把阴影部分看作两个三角形，
左边阴影三角形面积：
$S_{左阴}=（10-6）×6÷2=12$（$cm^2$），
右边阴影三角形面积：
$S_{右阴}=（10+8）×8÷2=72$（$cm^2$），
梯形面积：
$S_{梯}=(6+10)×6÷2=48$（$cm^2$），
$S_{阴影}=S_{右阴}+S_{左阴}-S_{梯}=54$（$cm^2$）。
综上，阴影部分的面积是$54cm^2$。

1. 下面是实验小学所在街区的平面图。

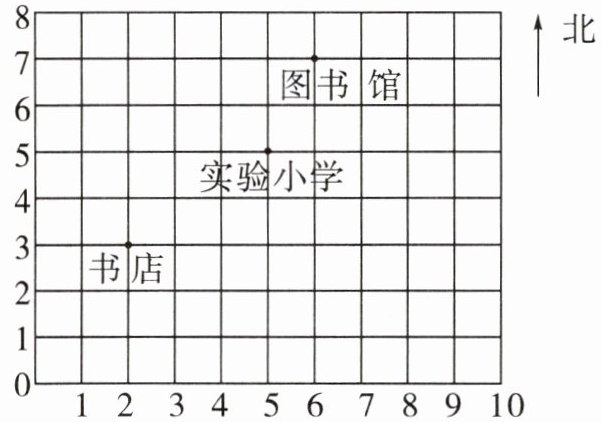
(1)用数对表示下列场所的位置。
实验小学((5,5))
图书馆((6,7))
书店((2,3))
(2)在图中标出下列场所的位置。
商店$(1,6)$ 电影院$(3,2)$
体育场$(7,1)$ 公园$(9,5)$

答案： 1.
(1)(5,5) (6,7) (2,3)
(2)