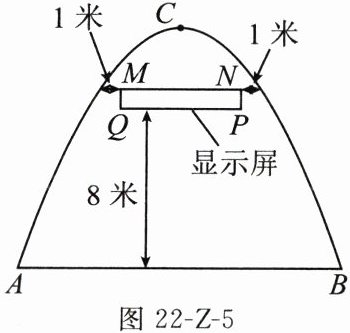
16. 如图22-Z-5,为了提醒司机安全驾驶,要在隧道中安装矩形电子显示屏.已知隧道截面为抛物线形,水平路面宽$AB=16$米,抛物线的顶点$C$到$AB$的距离为12米.根据计划,矩形显示屏$MNPQ$的宽$MQ$为1米,为了确保行车安全,显示屏底部距离地面至少8米.若显示屏距离左右墙壁各留至少1米的维修空间,则该矩形显示屏$MNPQ$的长$QP$最大为____米.

答案:
6 [解析] 如图,建立平面直角坐标系. 由题意知顶点 $C$ 的坐标为 $(0,12)$,$B(8,0)$,$\therefore$ 可设抛物线的解析式为 $y=m x^{2}+12$. 将 $B(8,0)$ 代入,得 $0=64 m+12$,解得 $m=-\frac{3}{16}$,$\therefore$ 抛物线的解析式为 $y=-\frac{3}{16} x^{2}+12$. $\because$ 显示屏底部距离地面至少 8 米,$M Q=1$ 米,$\therefore$ 令 $y=8+1=9$,则 $9=-\frac{3}{16} x^{2}+12$,解得 $x_{1}=4$,$x_{2}=-4$. $\therefore D(4,9)$. 又显示屏距离左右墙壁各留至少 1 米的维修空间,$\therefore$ 矩形显示屏 $M N P Q$ 的长 $Q P$ 的最大长度为 $2 ×(4-1)=6$ (米). 故答案为 6.

6 [解析] 如图,建立平面直角坐标系. 由题意知顶点 $C$ 的坐标为 $(0,12)$,$B(8,0)$,$\therefore$ 可设抛物线的解析式为 $y=m x^{2}+12$. 将 $B(8,0)$ 代入,得 $0=64 m+12$,解得 $m=-\frac{3}{16}$,$\therefore$ 抛物线的解析式为 $y=-\frac{3}{16} x^{2}+12$. $\because$ 显示屏底部距离地面至少 8 米,$M Q=1$ 米,$\therefore$ 令 $y=8+1=9$,则 $9=-\frac{3}{16} x^{2}+12$,解得 $x_{1}=4$,$x_{2}=-4$. $\therefore D(4,9)$. 又显示屏距离左右墙壁各留至少 1 米的维修空间,$\therefore$ 矩形显示屏 $M N P Q$ 的长 $Q P$ 的最大长度为 $2 ×(4-1)=6$ (米). 故答案为 6.

17. (6分)已知抛物线$y=mx^{2}-2mx+n$过点$A(1,-3),B(-1,1)$.
(1)求该抛物线的解析式;
(2)判断点$P(2,5)$是否在该抛物线上,并说明理由.
(1)求该抛物线的解析式;
(2)判断点$P(2,5)$是否在该抛物线上,并说明理由.
答案:
解:
(1) 根据题意,得 $\left\{\begin{array}{l}m-2 m+n=-3, \\ m+2 m+n=1,\end{array}\right.$
解得 $\left\{\begin{array}{l}m=1, \\ n=-2,\end{array}\right.$
$\therefore$ 该抛物线的解析式为 $y=x^{2}-2 x-2$.
(2) 不在.
理由如下: 当 $x=2$ 时,$y=x^{2}-2 x-2=2^{2}-2 × 2-2=-2 \neq 5$,$\therefore$ 点 $P(2,5)$ 不在该抛物线上.
(1) 根据题意,得 $\left\{\begin{array}{l}m-2 m+n=-3, \\ m+2 m+n=1,\end{array}\right.$
解得 $\left\{\begin{array}{l}m=1, \\ n=-2,\end{array}\right.$
$\therefore$ 该抛物线的解析式为 $y=x^{2}-2 x-2$.
(2) 不在.
理由如下: 当 $x=2$ 时,$y=x^{2}-2 x-2=2^{2}-2 × 2-2=-2 \neq 5$,$\therefore$ 点 $P(2,5)$ 不在该抛物线上.
18. (6分)已知抛物线$y=-x^{2}-6x+7$与$x$轴交于点$A,B$(点$A$在点$B$的左侧),与$y$轴交于点$C$.
(1)求点$A,B$的坐标;
(2)求$\triangle ABC$的面积.
(1)求点$A,B$的坐标;
(2)求$\triangle ABC$的面积.
答案:
解:
(1) 当 $y=0$ 时,$-x^{2}-6 x+7=0$,
解得 $x_{1}=-7$,$x_{2}=1$,
$\therefore$ 点 $A$ 的坐标为 $(-7,0)$,点 $B$ 的坐标为 $(1,0)$.
(2) 当 $x=0$ 时,$y=-x^{2}-6 x+7=7$,
$\therefore$ 点 $C$ 的坐标为 $(0,7)$,
$\therefore \triangle A B C$ 的面积 $=\frac{1}{2} ×(1+7) × 7=28$.
(1) 当 $y=0$ 时,$-x^{2}-6 x+7=0$,
解得 $x_{1}=-7$,$x_{2}=1$,
$\therefore$ 点 $A$ 的坐标为 $(-7,0)$,点 $B$ 的坐标为 $(1,0)$.
(2) 当 $x=0$ 时,$y=-x^{2}-6 x+7=7$,
$\therefore$ 点 $C$ 的坐标为 $(0,7)$,
$\therefore \triangle A B C$ 的面积 $=\frac{1}{2} ×(1+7) × 7=28$.
查看更多完整答案,请扫码查看


