《2025年全品学练考九年级数学上册人教版》

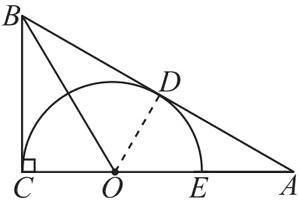
19. (6分)如图24-Z-16,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$O$为$AC$边上一点,连接$OB$.以$OC$为半径的半圆$O$与$AB$边相切于点$D$,交$AC$边于点$E$.
(1)求证:$BC = BD$;
(2)若$OB = OA$,$AE = 2$,求半圆$O$的半径.

答案：
解:
(1) 证明: 如图, 连接 OD.
∵AB 是半圆 O 的切线, D 为切点,
∴∠ODB = 90°.
在 Rt△OCB 和 Rt△ODB 中, $\begin{cases} OC = OD, \\ OB = OB, \end{cases}$
∴Rt△OCB ≌ Rt△ODB (HL),
∴BC = BD.

(2)
∵OB = OA,
∴∠OBD = ∠A.
由
(1) 知 Rt△OCB ≌ Rt△ODB,
∴∠OBC = ∠OBD,
∴∠OBC = ∠OBD = ∠A.
∵∠OBC + ∠OBD + ∠A = 90°,
∴∠OBC = ∠OBD = ∠A = 30°,
∴OD = $\frac{1}{2}$OA.
又
∵OD = OE,
∴OE = $\frac{1}{2}$OA,
∴OE = AE = 2,
∴半圆 O 的半径为 2.

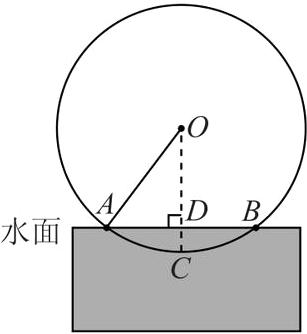
20. (8分)“筒车”是一种以水流作动力,取水灌田的工具.明朝科学家徐光启在《农政全书》中用图画描绘了“筒车”的工作原理.如图24-Z-17,“筒车”盛水筒的运行轨迹是以轴心$O$为圆心的圆,已知圆心$O$始终在水面上方,且当圆被水面截得的弦$AB$为6米时,水面下盛水筒的最大深度为1米(即水面下方部分圆上一点距离水面的最大距离).
(1)求该圆的半径;
(2)若水面上涨导致圆被水面截得的弦$AB$从原来的6米变为8米,则水面下盛水筒的最大深度为多少米?

答案：
解:
(1) 如图, 过点 O 作 OC⊥AB 于点 D, 交⊙O 于点 C, 则 AD = $\frac{1}{2}$AB = 3 米, CD = 1 米.

设⊙O 的半径为 r 米.
在 Rt△AOD 中, 由勾股定理, 得 AD² + OD² = OA²,
即 3² + (r - 1)² = r², 解得 r = 5,
∴该圆的半径为 5 米.
(2) 当 AB = 8 米时, AD = $\frac{1}{2}$AB = 4 米.
在 Rt△AOD 中, 由勾股定理, 得 OD = $\sqrt{OA^{2} - AD^{2}}$ = $\sqrt{5^{2} - 4^{2}}$ = 3(米),
∴CD = OC - OD = 5 - 3 = 2(米).
答: 水面下盛水筒的最大深度为 2 米.