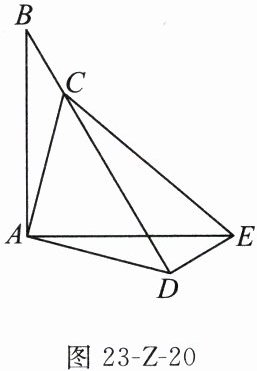
21. (8 分)如图 23-Z-20,在 $ \triangle ABC $ 中,$ \angle ACB=135^{\circ},BC=1,AC=2 $,将 $ \triangle ABC $ 绕点 $ A $ 顺时针旋转 $ 90^{\circ} $ 得到 $ \triangle AED $,连接 $ CD,CE $.
(1)求 $ CD $ 的长;
(2)求四边形 $ ACED $ 的面积.
(1)求 $ CD $ 的长;
(2)求四边形 $ ACED $ 的面积.

答案:
解:
(1) 根据旋转的性质,得 $ AD = AC = 2 $,$ \angle CAD = 90^{\circ} $,
∴ $ CD = \sqrt{AC^{2} + AD^{2}} = \sqrt{2^{2} + 2^{2}} = 2\sqrt{2} $.
(2) 根据旋转的性质,得 $ \angle ADE = \angle ACB = 135^{\circ} $,$ DE = BC = 1 $.
∵ $ \angle CAD = 90^{\circ} $,$ AC = AD $,
∴ $ \angle ADC = 45^{\circ} $,
∴ $ \angle CDE = \angle ADE - \angle ADC = 135^{\circ} - 45^{\circ} = 90^{\circ} $,
∴ $ S_{四边形ACED} = S_{\triangle ACD} + S_{\triangle CDE} = \frac{1}{2}AC \cdot AD + \frac{1}{2}CD \cdot DE = \frac{1}{2} × 2 × 2 + \frac{1}{2} × 2\sqrt{2} × 1 = 2 + \sqrt{2} $.
(1) 根据旋转的性质,得 $ AD = AC = 2 $,$ \angle CAD = 90^{\circ} $,
∴ $ CD = \sqrt{AC^{2} + AD^{2}} = \sqrt{2^{2} + 2^{2}} = 2\sqrt{2} $.
(2) 根据旋转的性质,得 $ \angle ADE = \angle ACB = 135^{\circ} $,$ DE = BC = 1 $.
∵ $ \angle CAD = 90^{\circ} $,$ AC = AD $,
∴ $ \angle ADC = 45^{\circ} $,
∴ $ \angle CDE = \angle ADE - \angle ADC = 135^{\circ} - 45^{\circ} = 90^{\circ} $,
∴ $ S_{四边形ACED} = S_{\triangle ACD} + S_{\triangle CDE} = \frac{1}{2}AC \cdot AD + \frac{1}{2}CD \cdot DE = \frac{1}{2} × 2 × 2 + \frac{1}{2} × 2\sqrt{2} × 1 = 2 + \sqrt{2} $.
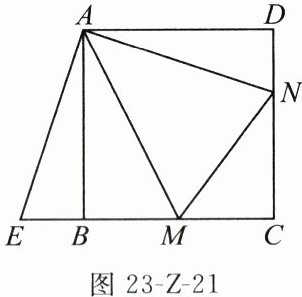
22. (8 分)如图 23-Z-21,点 $ M,N $ 分别在正方形 $ ABCD $ 的边 $ BC $,$ CD $ 上,且 $ \angle MAN=45^{\circ} $. 把 $ \triangle ADN $ 绕点 $ A $ 顺时针旋转 $ 90^{\circ} $ 得到 $ \triangle ABE $,此时点 $ E,B,M $ 共线.
(1)求证:$ \triangle AEM\cong\triangle ANM $;
(2)若正方形 $ ABCD $ 的边长为 6,$ DN=2 $,求 $ BM $ 的长.
(1)求证:$ \triangle AEM\cong\triangle ANM $;
(2)若正方形 $ ABCD $ 的边长为 6,$ DN=2 $,求 $ BM $ 的长.

答案:
解:
(1) 证明:由旋转的性质,得 $ AE = AN $,$ \angle BAE = \angle DAN $.
∵四边形 $ ABCD $ 是正方形,
∴ $ \angle BAD = 90^{\circ} $,即 $ \angle BAN + \angle DAN = 90^{\circ} $,
∴ $ \angle BAN + \angle BAE = 90^{\circ} $,即 $ \angle EAN = 90^{\circ} $.
∵ $ \angle MAN = 45^{\circ} $,
∴ $ \angle MAE = \angle EAN - \angle MAN = 90^{\circ} - 45^{\circ} = 45^{\circ} $.
在 $ \triangle AEM $ 和 $ \triangle ANM $ 中,
$\left\{ \begin{array}{l} AE = AN, \\ \angle MAE = \angle MAN = 45^{\circ}, \\ AM = AM, \end{array} \right.$
∴ $ \triangle AEM \cong \triangle ANM(SAS) $.
(2) 由旋转的性质可得 $ BE = DN = 2 $.
由
(1)得 $ \triangle AEM \cong \triangle ANM $,
∴ $ EM = NM $.
设 $ BM = x $,则 $ NM = EM = x + 2 $.
∵正方形 $ ABCD $ 的边长为 6,
∴ $ BC = CD = 6 $,$ \angle C = 90^{\circ} $,
∴ $ CM = BC - BM = 6 - x $,$ CN = CD - DN = 4 $.
在 $ Rt\triangle CMN $ 中,由勾股定理,得 $ CM^{2} + CN^{2} = NM^{2} $,
∴ $ (6 - x)^{2} + 4^{2} = (x + 2)^{2} $,
解得 $ x = 3 $,即 $ BM = 3 $.
(1) 证明:由旋转的性质,得 $ AE = AN $,$ \angle BAE = \angle DAN $.
∵四边形 $ ABCD $ 是正方形,
∴ $ \angle BAD = 90^{\circ} $,即 $ \angle BAN + \angle DAN = 90^{\circ} $,
∴ $ \angle BAN + \angle BAE = 90^{\circ} $,即 $ \angle EAN = 90^{\circ} $.
∵ $ \angle MAN = 45^{\circ} $,
∴ $ \angle MAE = \angle EAN - \angle MAN = 90^{\circ} - 45^{\circ} = 45^{\circ} $.
在 $ \triangle AEM $ 和 $ \triangle ANM $ 中,
$\left\{ \begin{array}{l} AE = AN, \\ \angle MAE = \angle MAN = 45^{\circ}, \\ AM = AM, \end{array} \right.$
∴ $ \triangle AEM \cong \triangle ANM(SAS) $.
(2) 由旋转的性质可得 $ BE = DN = 2 $.
由
(1)得 $ \triangle AEM \cong \triangle ANM $,
∴ $ EM = NM $.
设 $ BM = x $,则 $ NM = EM = x + 2 $.
∵正方形 $ ABCD $ 的边长为 6,
∴ $ BC = CD = 6 $,$ \angle C = 90^{\circ} $,
∴ $ CM = BC - BM = 6 - x $,$ CN = CD - DN = 4 $.
在 $ Rt\triangle CMN $ 中,由勾股定理,得 $ CM^{2} + CN^{2} = NM^{2} $,
∴ $ (6 - x)^{2} + 4^{2} = (x + 2)^{2} $,
解得 $ x = 3 $,即 $ BM = 3 $.
查看更多完整答案,请扫码查看


