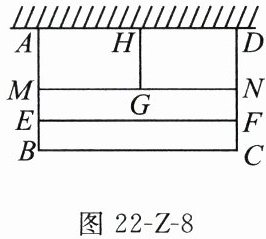
21. (8分)如图22-Z-8,某小区有一块靠墙(墙的长度不限)的矩形空地$ABCD$,为美化环境,用总长为100m的篱笆围成四块矩形花圃(靠墙一侧不用篱笆,篱笆的厚度不计).
(1)若四块矩形花圃的面积相等,求证:$AE=3BE$;
(2)在(1)的条件下,设$BC$的长度为$x$m,矩形区域$ABCD$的面积为$y$m²,求$y$与$x$之间的函数关系式,并写出自变量$x$的取值范围.
(1)若四块矩形花圃的面积相等,求证:$AE=3BE$;
(2)在(1)的条件下,设$BC$的长度为$x$m,矩形区域$ABCD$的面积为$y$m²,求$y$与$x$之间的函数关系式,并写出自变量$x$的取值范围.

答案:
解:
(1) 证明: $\because$ 四块矩形花圃的面积相等,
$\therefore S_{\text {矩形 } M E F N}=S_{\text {矩形 } E B C F}$,$S_{\text {矩形 } A M N D}=2 S_{\text {矩形 } M E F N}$,
$\therefore M E=B E$,$A M=2 M E$,
$\therefore A E=3 M E=3 B E$.
(2) $\because$ 篱笆总长为 $100 \mathrm{~m}$,
$\therefore 2 A B+G H+3 B C=100$,
即 $2 A B+\frac{1}{2} A B+3 B C=100$,
$\therefore A B=40-\frac{6}{5} B C$.
$\because B C$ 的长度为 $x \mathrm{~m}$,矩形区域 $A B C D$ 的面积为 $y \mathrm{~m}^{2}$,
$\therefore y=B C \cdot A B=x\left(40-\frac{6}{5} x\right)=-\frac{6}{5} x^{2}+40 x$.
由题意可得 $\left\{\begin{array}{l}x>0, \\ 40-\frac{6}{5} x>0,\end{array}\right.$
解得 $0<x<\frac{100}{3}$,
$\therefore y=-\frac{6}{5} x^{2}+40 x\left(0<x<\frac{100}{3}\right)$.
(1) 证明: $\because$ 四块矩形花圃的面积相等,
$\therefore S_{\text {矩形 } M E F N}=S_{\text {矩形 } E B C F}$,$S_{\text {矩形 } A M N D}=2 S_{\text {矩形 } M E F N}$,
$\therefore M E=B E$,$A M=2 M E$,
$\therefore A E=3 M E=3 B E$.
(2) $\because$ 篱笆总长为 $100 \mathrm{~m}$,
$\therefore 2 A B+G H+3 B C=100$,
即 $2 A B+\frac{1}{2} A B+3 B C=100$,
$\therefore A B=40-\frac{6}{5} B C$.
$\because B C$ 的长度为 $x \mathrm{~m}$,矩形区域 $A B C D$ 的面积为 $y \mathrm{~m}^{2}$,
$\therefore y=B C \cdot A B=x\left(40-\frac{6}{5} x\right)=-\frac{6}{5} x^{2}+40 x$.
由题意可得 $\left\{\begin{array}{l}x>0, \\ 40-\frac{6}{5} x>0,\end{array}\right.$
解得 $0<x<\frac{100}{3}$,
$\therefore y=-\frac{6}{5} x^{2}+40 x\left(0<x<\frac{100}{3}\right)$.
22. (8分)某工厂生产一种产品,经市场调查发现,该产品每月的销售量$y$(件)与每件的售价$x$(万元)之间满足一次函数关系,部分数据如下表:
| 每件的售价$x$/万元 | $\cdots$ | 24 | 26 | 28 | 30 | 32 | $\cdots$ |
| --- | --- | --- | --- | --- | --- | --- | --- |
| 每月的销售量$y$/件 | $\cdots$ | 52 | 48 | 44 | 40 | 36 | $\cdots$ |
(1)求$y$与$x$之间的函数解析式(不必写自变量的取值范围).
(2)已知该产品三月份每件的售价为35万元,利润为450万元.
①求三月份每件产品的成本是多少万元;
②四月份工厂为了降低成本,提高产品质量,投资了450万元改进设备和革新技术,使每件产品的成本比三月份下降了14万元.若四月份每件产品的售价至少为25万元,且不高于30万元,求这个月获得的利润$w$(万元)与每件的售价$x$(万元)之间的函数解析式,并求最少利润是多少万元.
| 每件的售价$x$/万元 | $\cdots$ | 24 | 26 | 28 | 30 | 32 | $\cdots$ |
| --- | --- | --- | --- | --- | --- | --- | --- |
| 每月的销售量$y$/件 | $\cdots$ | 52 | 48 | 44 | 40 | 36 | $\cdots$ |
(1)求$y$与$x$之间的函数解析式(不必写自变量的取值范围).
(2)已知该产品三月份每件的售价为35万元,利润为450万元.
①求三月份每件产品的成本是多少万元;
②四月份工厂为了降低成本,提高产品质量,投资了450万元改进设备和革新技术,使每件产品的成本比三月份下降了14万元.若四月份每件产品的售价至少为25万元,且不高于30万元,求这个月获得的利润$w$(万元)与每件的售价$x$(万元)之间的函数解析式,并求最少利润是多少万元.
答案:
解:
(1) 在表格中取点 $(30,40)$,$(32,36)$,
设 $y$ 与 $x$ 之间的函数解析式为 $y=k x+b$,
则 $\left\{\begin{array}{l}40=30 k+b, \\ 36=32 k+b,\end{array}\right.$ 解得 $\left\{\begin{array}{l}k=-2, \\ b=100,\end{array}\right.$
则 $y$ 与 $x$ 之间的函数解析式为 $y=-2 x+100$.
(2) ①设三月份每件产品的成本是 $m$ 万元.
当 $x=35$ 时,$y=-2 x+100=30$.
由题意,得 $450=30(35-m)$,
解得 $m=20$,
即三月份每件产品的成本是 20 万元.
② $\because$ 四月份每件产品的成本比三月份下降了 14 万元,$\therefore$ 四月份每件产品的成本为 $20-14=6$ (万元).
由题意,得 $w=y(x-6)-450=(-2 x+100) \cdot(x-6)-450=-2 x^{2}+112 x-1050(25 \leqslant x \leqslant 30)$.
$\because-2<0$,$\therefore$ 抛物线的开口向下.
$\because$ 抛物线的对称轴为直线 $x=-\frac{112}{2 ×(-2)}=28$,$25 \leqslant x \leqslant 30$,
$\therefore$ 当 $x=25$ 时,$w$ 取得最小值,
此时 $w=-2 × 25^{2}+112 × 25-1050=500$,
即四月份的最少利润是 500 万元.
(1) 在表格中取点 $(30,40)$,$(32,36)$,
设 $y$ 与 $x$ 之间的函数解析式为 $y=k x+b$,
则 $\left\{\begin{array}{l}40=30 k+b, \\ 36=32 k+b,\end{array}\right.$ 解得 $\left\{\begin{array}{l}k=-2, \\ b=100,\end{array}\right.$
则 $y$ 与 $x$ 之间的函数解析式为 $y=-2 x+100$.
(2) ①设三月份每件产品的成本是 $m$ 万元.
当 $x=35$ 时,$y=-2 x+100=30$.
由题意,得 $450=30(35-m)$,
解得 $m=20$,
即三月份每件产品的成本是 20 万元.
② $\because$ 四月份每件产品的成本比三月份下降了 14 万元,$\therefore$ 四月份每件产品的成本为 $20-14=6$ (万元).
由题意,得 $w=y(x-6)-450=(-2 x+100) \cdot(x-6)-450=-2 x^{2}+112 x-1050(25 \leqslant x \leqslant 30)$.
$\because-2<0$,$\therefore$ 抛物线的开口向下.
$\because$ 抛物线的对称轴为直线 $x=-\frac{112}{2 ×(-2)}=28$,$25 \leqslant x \leqslant 30$,
$\therefore$ 当 $x=25$ 时,$w$ 取得最小值,
此时 $w=-2 × 25^{2}+112 × 25-1050=500$,
即四月份的最少利润是 500 万元.
查看更多完整答案,请扫码查看


