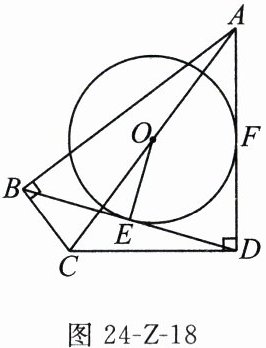
21. (8分)如图24-Z-18,在四边形$ABCD$中,$\angle ABC = \angle ADC = 90^{\circ}$,$O$,$E$分别为对角线$AC$,$BD$的中点,连接$OE$,以点$O$为圆心,$OE$为半径作圆.
(1)求证:$BD$与$\odot O$相切;
(2)若$\odot O$与$AD$相切于点$F$,$BD = 8$,$AC = 10$,求$CD$的长.
(1)求证:$BD$与$\odot O$相切;
(2)若$\odot O$与$AD$相切于点$F$,$BD = 8$,$AC = 10$,求$CD$的长.

答案:
解:
(1) 证明: 连接 OB, OD, 如图.
∵∠ABC = ∠ADC = 90°, O 为 AC 的中点,
∴OB, OD 分别为 Rt△ACB 和 Rt△ACD 的斜边上的中线,
∴OB = OD = $\frac{1}{2}$AC.
∵E 为 BD 的中点,
∴OE⊥BD.
又
∵OE 是⊙O 的半径,
∴BD 与⊙O 相切.
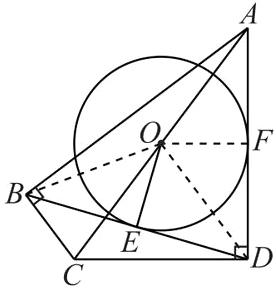
(2) 连接 OF, 如图.
∵BD = 8, AC = 10, E 是 BD 的中点,
∴OD = $\frac{1}{2}$AC = 5, DE = $\frac{1}{2}$BD = 4,
∴OE = $\sqrt{OD^{2} - DE^{2}}$ = 3.
∵AD 是⊙O 的切线,
∴OF⊥AD.
∵OD = $\frac{1}{2}$AC = OA,
∴FA = FD.
又
∵OA = OC,
∴OF 为△ACD 的中位线,
∴CD = 2OF = 2OE = 6.
解:
(1) 证明: 连接 OB, OD, 如图.
∵∠ABC = ∠ADC = 90°, O 为 AC 的中点,
∴OB, OD 分别为 Rt△ACB 和 Rt△ACD 的斜边上的中线,
∴OB = OD = $\frac{1}{2}$AC.
∵E 为 BD 的中点,
∴OE⊥BD.
又
∵OE 是⊙O 的半径,
∴BD 与⊙O 相切.

(2) 连接 OF, 如图.
∵BD = 8, AC = 10, E 是 BD 的中点,
∴OD = $\frac{1}{2}$AC = 5, DE = $\frac{1}{2}$BD = 4,
∴OE = $\sqrt{OD^{2} - DE^{2}}$ = 3.
∵AD 是⊙O 的切线,
∴OF⊥AD.
∵OD = $\frac{1}{2}$AC = OA,
∴FA = FD.
又
∵OA = OC,
∴OF 为△ACD 的中位线,
∴CD = 2OF = 2OE = 6.
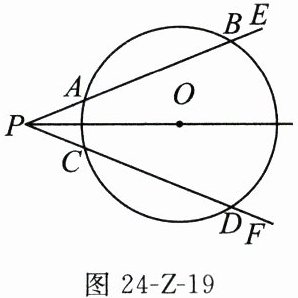
22. (8分)如图24-Z-19,$O$是$\angle EPF$的平分线上一点,$\odot O$与角的两边分别交于点$A$,$B$,$C$,$D$.
(1)求证:$AB = CD$.
(2)若角的顶点$P$在$\odot O$上或$\odot O$内,则(1)中的结论还成立吗?若不成立,请说明理由;若成立,请加以证明.
(1)求证:$AB = CD$.
(2)若角的顶点$P$在$\odot O$上或$\odot O$内,则(1)中的结论还成立吗?若不成立,请说明理由;若成立,请加以证明.

答案:
解:
(1) 证明: 如图①, 连接 OA, OB, OC, OD. 过点 O 作 OM⊥AB 于点 M, ON⊥CD 于点 N,
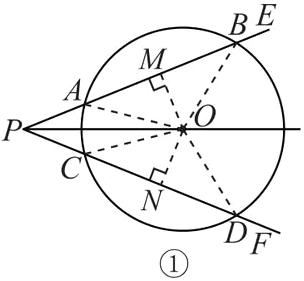
则 ∠OMB = ∠OND = 90°, AB = 2BM, CD = 2DN.
∵PO 平分 ∠EPF, OM⊥AB, ON⊥CD,
∴OM = ON.
在 Rt△OMB 和 Rt△OND 中,
$\begin{cases} OB = OD, \\ OM = ON, \end{cases}$
∴Rt△OMB ≌ Rt△OND (HL),
∴BM = DN,
∴AB = CD.
(2) 成立.
证明: 如图②, 当点 P 在⊙O 上时, 过点 O 作 OM⊥AB 于点 M, ON⊥CD 于点 N.
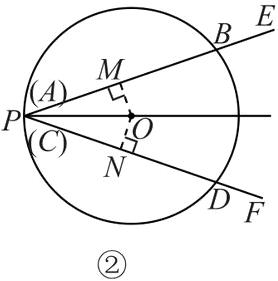
同
(1) 可得 BM = DN, AB = 2BM, CD = 2DN,
∴AB = CD;
如图③, 当点 P 在⊙O 内时, 过点 O 作 OM⊥AB 于点 M, ON⊥CD 于点 N.
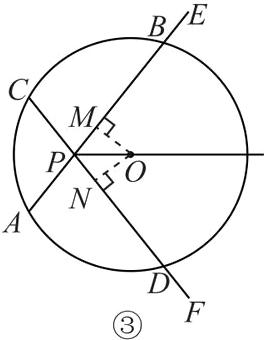
同
(1) 可得 BM = DN, AB = 2BM, CD = 2DN,
∴AB = CD.
解:
(1) 证明: 如图①, 连接 OA, OB, OC, OD. 过点 O 作 OM⊥AB 于点 M, ON⊥CD 于点 N,

则 ∠OMB = ∠OND = 90°, AB = 2BM, CD = 2DN.
∵PO 平分 ∠EPF, OM⊥AB, ON⊥CD,
∴OM = ON.
在 Rt△OMB 和 Rt△OND 中,
$\begin{cases} OB = OD, \\ OM = ON, \end{cases}$
∴Rt△OMB ≌ Rt△OND (HL),
∴BM = DN,
∴AB = CD.
(2) 成立.
证明: 如图②, 当点 P 在⊙O 上时, 过点 O 作 OM⊥AB 于点 M, ON⊥CD 于点 N.

同
(1) 可得 BM = DN, AB = 2BM, CD = 2DN,
∴AB = CD;
如图③, 当点 P 在⊙O 内时, 过点 O 作 OM⊥AB 于点 M, ON⊥CD 于点 N.

同
(1) 可得 BM = DN, AB = 2BM, CD = 2DN,
∴AB = CD.
查看更多完整答案,请扫码查看


