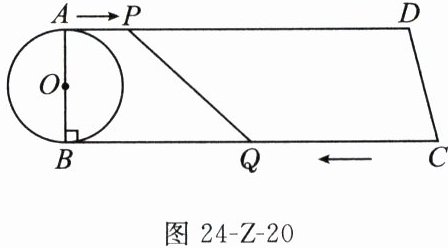
23. (10分)如图24-Z-20,在四边形$ABCD$中,$AD// BC$,$\angle B = 90^{\circ}$,$AB = 8 cm$,$AD = 24 cm$,$BC = 26 cm$,$AB$为$\odot O$的直径.动点$P$从点$A$开始沿$AD$边向终点$D$以$1 cm/s$的速度运动,动点$Q$从点$C$开始沿$CB$边向终点$B$以$3 cm/s$的速度运动,$P$,$Q$两点同时出发,当其中一点到达终点时,另一点也随之停止运动.当运动时间为多少时,直线$PQ$与$\odot O$相切、相离、相交?

答案:
解: 设运动时间为 t s 时, 直线 PQ 与⊙O 相切于点 G, 过点 P 作 PH⊥BC 于点 H, 如图,

则四边形 ABHP 为矩形,
∴PH = AB = 8, BH = AP = t.
由题意, 得 BQ = 26 - 3t,
∴HQ = |t - (26 - 3t)| = |4t - 26|.
由切线长定理, 得 AP = PG, QG = BQ,
则 PQ = PG + QG = AP + BQ = t + 26 - 3t = 26 - 2t.
在 Rt△PQH 中, 由勾股定理, 得 PQ² = PH² + HQ²,
即 (26 - 2t)² = 8² + (4t - 26)²,
化简, 得 3t² - 26t + 16 = 0,
解得 t₁ = $\frac{2}{3}$, t₂ = 8,
∴当 t = $\frac{2}{3}$ 或 t = 8 时, 直线 PQ 与⊙O 相切.
∵当 t = 0 时, 直线 PQ 与⊙O 相交,
当 t = $\frac{26}{3}$ 时, 点 Q 运动到点 B, 点 P 尚未运动到点 D, 但也停止运动, 直线 PQ 也与⊙O 相交,
∴可得以下结论:
当 t = $\frac{2}{3}$ 或 t = 8 时, 直线 PQ 与⊙O 相切;
当 $\frac{2}{3}$ < t < 8 时, 直线 PQ 与⊙O 相离;
当 0 ≤ t < $\frac{2}{3}$ 或 8 < t ≤ $\frac{26}{3}$ 时, 直线 PQ 与⊙O 相交.
解: 设运动时间为 t s 时, 直线 PQ 与⊙O 相切于点 G, 过点 P 作 PH⊥BC 于点 H, 如图,

则四边形 ABHP 为矩形,
∴PH = AB = 8, BH = AP = t.
由题意, 得 BQ = 26 - 3t,
∴HQ = |t - (26 - 3t)| = |4t - 26|.
由切线长定理, 得 AP = PG, QG = BQ,
则 PQ = PG + QG = AP + BQ = t + 26 - 3t = 26 - 2t.
在 Rt△PQH 中, 由勾股定理, 得 PQ² = PH² + HQ²,
即 (26 - 2t)² = 8² + (4t - 26)²,
化简, 得 3t² - 26t + 16 = 0,
解得 t₁ = $\frac{2}{3}$, t₂ = 8,
∴当 t = $\frac{2}{3}$ 或 t = 8 时, 直线 PQ 与⊙O 相切.
∵当 t = 0 时, 直线 PQ 与⊙O 相交,
当 t = $\frac{26}{3}$ 时, 点 Q 运动到点 B, 点 P 尚未运动到点 D, 但也停止运动, 直线 PQ 也与⊙O 相交,
∴可得以下结论:
当 t = $\frac{2}{3}$ 或 t = 8 时, 直线 PQ 与⊙O 相切;
当 $\frac{2}{3}$ < t < 8 时, 直线 PQ 与⊙O 相离;
当 0 ≤ t < $\frac{2}{3}$ 或 8 < t ≤ $\frac{26}{3}$ 时, 直线 PQ 与⊙O 相交.
查看更多完整答案,请扫码查看


