15. 如图24-Z-12,在边长为2的正方形$ABCD$中,对角线$AC$的中点为$O$,分别以点$A$,$C$为圆心,以$AO$长为半径画弧,分别与正方形的边相交,则图中阴影部分的面积为________.(结果保留$\pi$)


答案:
4 - π [解析] 如图,
∵正方形 ABCD 的边长为 2, 对角线 AC 的中点为 O,
∴AO = $\frac{1}{2}$AC = $\frac{1}{2}$×$\sqrt{2^{2} + 2^{2}}$ = $\sqrt{2}$.
∵S_{正方形 ABCD} = 2² = 4, S_{扇形 AEF} = $\frac{90π×(\sqrt{2})^{2}}{360}$ = $\frac{π}{2}$,
∴S_{阴影} = 4 - 2×$\frac{π}{2}$ = 4 - π.

4 - π [解析] 如图,
∵正方形 ABCD 的边长为 2, 对角线 AC 的中点为 O,
∴AO = $\frac{1}{2}$AC = $\frac{1}{2}$×$\sqrt{2^{2} + 2^{2}}$ = $\sqrt{2}$.
∵S_{正方形 ABCD} = 2² = 4, S_{扇形 AEF} = $\frac{90π×(\sqrt{2})^{2}}{360}$ = $\frac{π}{2}$,
∴S_{阴影} = 4 - 2×$\frac{π}{2}$ = 4 - π.

16. 如图24-Z-13所示,$\odot O$的半径是2,直线$l$与$\odot O$相交于$A$,$B$两点,$M$,$N$是$\odot O$上的两个动点,且在直线$l$的异侧.若$\angle AMB = 45^{\circ}$,则四边形$MANB$面积的最大值是________.
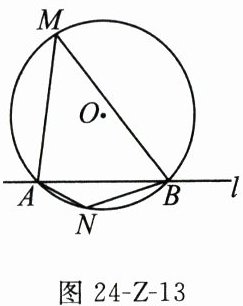
答案:
4$\sqrt{2}$ [解析] 如图, 过点 O 作 OC⊥AB 于点 C, 交⊙O 于 D, E 两点, 连接 OA, OB, DA, DB, EA, EB.
∵∠AMB = 45°,
∴∠AOB = 2∠AMB = 90°.
又
∵OA = OB = 2,
∴AB = $\sqrt{OA^{2} + OB^{2}}$ = 2$\sqrt{2}$.
∵S_{四边形 MANB} = S_{△MAB} + S_{△NAB},
又当点 M 到 AB 的距离最大时, △MAB 的面积最大; 当点 N 到 AB 的距离最大时, △NAB 的面积最大,
∴当点 M 运动到点 D, 点 N 运动到点 E 时, 四边形 MANB 的面积最大, 此时 S_{四边形 MANB} = S_{四边形 DAEB} = S_{△DAB} + S_{△EAB} = $\frac{1}{2}$AB·CD + $\frac{1}{2}$AB·CE = $\frac{1}{2}$AB·(CD + CE) = $\frac{1}{2}$AB·DE = $\frac{1}{2}$×2$\sqrt{2}$×4 = 4$\sqrt{2}$.

4$\sqrt{2}$ [解析] 如图, 过点 O 作 OC⊥AB 于点 C, 交⊙O 于 D, E 两点, 连接 OA, OB, DA, DB, EA, EB.
∵∠AMB = 45°,
∴∠AOB = 2∠AMB = 90°.
又
∵OA = OB = 2,
∴AB = $\sqrt{OA^{2} + OB^{2}}$ = 2$\sqrt{2}$.
∵S_{四边形 MANB} = S_{△MAB} + S_{△NAB},
又当点 M 到 AB 的距离最大时, △MAB 的面积最大; 当点 N 到 AB 的距离最大时, △NAB 的面积最大,
∴当点 M 运动到点 D, 点 N 运动到点 E 时, 四边形 MANB 的面积最大, 此时 S_{四边形 MANB} = S_{四边形 DAEB} = S_{△DAB} + S_{△EAB} = $\frac{1}{2}$AB·CD + $\frac{1}{2}$AB·CE = $\frac{1}{2}$AB·(CD + CE) = $\frac{1}{2}$AB·DE = $\frac{1}{2}$×2$\sqrt{2}$×4 = 4$\sqrt{2}$.

17. (6分)如图24-Z-14,已知$OA = OB$,$AB$交$\odot O$于点$C$,$D$,$OE$是$\odot O$的半径,且$OE\perp AB$于点$F$.
(1)求证:$AC = BD$;
(2)若$CD = 10$,$EF = 3$,求$\odot O$的半径.
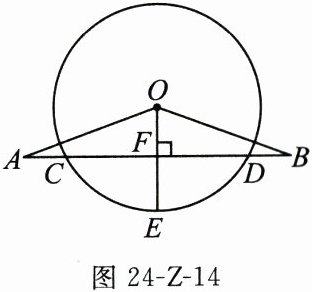
(1)求证:$AC = BD$;
(2)若$CD = 10$,$EF = 3$,求$\odot O$的半径.

答案:
解:
(1) 证明:
∵OA = OB, OE⊥AB 于点 F,
∴AF = BF.
∵OE 是⊙O 的半径, OE⊥AB,
∴CF = DF,
∴AF - CF = BF - DF, 即 AC = BD.
(2) 如图, 连接 OC.
∵OE 是⊙O 的半径, OE⊥AB,
∴CF = $\frac{1}{2}$CD = 5.
设⊙O 的半径是 r, 则 OF = r - 3.
在 Rt△OCF 中, 由勾股定理, 得 OC² = CF² + OF²,
即 r² = 5² + (r - 3)²,
解得 r = $\frac{17}{3}$,
∴⊙O 的半径是 $\frac{17}{3}$.

解:
(1) 证明:
∵OA = OB, OE⊥AB 于点 F,
∴AF = BF.
∵OE 是⊙O 的半径, OE⊥AB,
∴CF = DF,
∴AF - CF = BF - DF, 即 AC = BD.
(2) 如图, 连接 OC.
∵OE 是⊙O 的半径, OE⊥AB,
∴CF = $\frac{1}{2}$CD = 5.
设⊙O 的半径是 r, 则 OF = r - 3.
在 Rt△OCF 中, 由勾股定理, 得 OC² = CF² + OF²,
即 r² = 5² + (r - 3)²,
解得 r = $\frac{17}{3}$,
∴⊙O 的半径是 $\frac{17}{3}$.

18. (6分)如图24-Z-15,在$\odot O$中,$AB$是直径,$D$是$\odot O$上的一点,$C$是$\overset{\frown}{AD}$的中点,连接$AD$,$BC$,$\angle DAB = 30^{\circ}$.
(1)求$\angle ABC$的度数;
(2)若$AD = 8\sqrt{3}$,求$\overset{\frown}{AC}$的长(结果保留$\pi$).
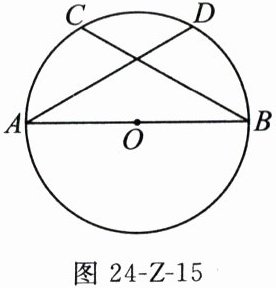
(1)求$\angle ABC$的度数;
(2)若$AD = 8\sqrt{3}$,求$\overset{\frown}{AC}$的长(结果保留$\pi$).

答案:
解:
(1) 如图, 连接 BD.
∵AB 是⊙O 的直径,
∴∠ADB = 90°.
∵∠DAB = 30°,
∴∠ABD = 90° - 30° = 60°.
∵C 是 $\overset{\frown}{AD}$ 的中点,
∴$\overset{\frown}{AC}$ = $\overset{\frown}{CD}$,
∴∠ABC = ∠DBC = $\frac{1}{2}$∠ABD = 30°.

(2) 如图, 连接 OC, 则 ∠AOC = 2∠ABC = 60°.
∵∠A = 30°, ∠ADB = 90°,
∴BD = $\frac{1}{2}$AB.
在 Rt△ABD 中, 由勾股定理, 得 AB² = BD² + AD², 即 AB² = ($\frac{1}{2}$AB)² + (8$\sqrt{3}$)²,
解得 AB = 16,
∴OA = 8,
∴$\overset{\frown}{AC}$ 的长 = $\frac{60π×8}{180}$ = $\frac{8}{3}$π.
解:
(1) 如图, 连接 BD.
∵AB 是⊙O 的直径,
∴∠ADB = 90°.
∵∠DAB = 30°,
∴∠ABD = 90° - 30° = 60°.
∵C 是 $\overset{\frown}{AD}$ 的中点,
∴$\overset{\frown}{AC}$ = $\overset{\frown}{CD}$,
∴∠ABC = ∠DBC = $\frac{1}{2}$∠ABD = 30°.

(2) 如图, 连接 OC, 则 ∠AOC = 2∠ABC = 60°.
∵∠A = 30°, ∠ADB = 90°,
∴BD = $\frac{1}{2}$AB.
在 Rt△ABD 中, 由勾股定理, 得 AB² = BD² + AD², 即 AB² = ($\frac{1}{2}$AB)² + (8$\sqrt{3}$)²,
解得 AB = 16,
∴OA = 8,
∴$\overset{\frown}{AC}$ 的长 = $\frac{60π×8}{180}$ = $\frac{8}{3}$π.
查看更多完整答案,请扫码查看


